题目内容
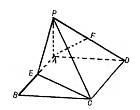
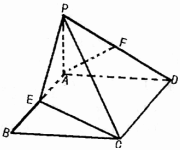
 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.(Ⅰ)求证:AF∥平面PCE;
(Ⅱ)若二面角P-CD-B为45°,AD=2,CD=3,求点F到平面PCE的距离.
分析:(Ⅰ)取PC中点M,连接ME、MF.由FM∥CD,FM=
CD,AE∥CD,AE=
CD,知AE∥FM,且AE=FM,由此能证明四边形AFME是平行四边形,从而得到AF∥平面PCE.
(Ⅱ)由PA⊥平面AC,CD⊥AD,根据三垂线定理知,CD⊥PD,故∠PDA是二面角P-CD-B的平面角,所以△PAD是等腰直角三角形,由AF⊥PD,AF⊥CD,得到面PEC⊥面PCD,由此入手能够求出点F到平面PCE的距离.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)由PA⊥平面AC,CD⊥AD,根据三垂线定理知,CD⊥PD,故∠PDA是二面角P-CD-B的平面角,所以△PAD是等腰直角三角形,由AF⊥PD,AF⊥CD,得到面PEC⊥面PCD,由此入手能够求出点F到平面PCE的距离.
解答:解:(Ⅰ)取PC中点M,连接ME、MF.
∵FM∥CD,FM=
CD,AE∥CD,AE=
CD,…(2分)
∴AE∥FM,且AE=FM,
即四边形AFME是平行四边形,
∴AF∥EM,∵AF?平在PCE,
∴AF∥平面PCE.…(4分)
(Ⅱ)∵PA⊥平面AC,CD⊥AD,
根据三垂线定理知,CD⊥PD,
∴∠PDA是二面角,
P-CD-B的平面角,则∠PDA=45°…(6分)
于是,△PAD是等腰直角三角形,
∵AF⊥PD,又AF⊥CD,
∴AF⊥面PCD.而EM∥AF,
∴EM⊥面PCD.又EM?平面PEC,
∴面PEC⊥面PCD.…(8分)
在面PCD内过F作FH⊥PC于H,
则FH为点F到平面PCE的距离.…(10分)
由已知,PD=2
,PF=
PD=
,PC=
.
∵△PFH∽△PCD,
∴
=
,FH=
.…(12分)
∵FM∥CD,FM=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE∥FM,且AE=FM,
即四边形AFME是平行四边形,
∴AF∥EM,∵AF?平在PCE,
∴AF∥平面PCE.…(4分)
(Ⅱ)∵PA⊥平面AC,CD⊥AD,
根据三垂线定理知,CD⊥PD,
∴∠PDA是二面角,
P-CD-B的平面角,则∠PDA=45°…(6分)
于是,△PAD是等腰直角三角形,
∵AF⊥PD,又AF⊥CD,
∴AF⊥面PCD.而EM∥AF,
∴EM⊥面PCD.又EM?平面PEC,
∴面PEC⊥面PCD.…(8分)
在面PCD内过F作FH⊥PC于H,
则FH为点F到平面PCE的距离.…(10分)
由已知,PD=2
| 2 |
| 1 |
| 2 |
| 2 |
| 17 |
∵△PFH∽△PCD,
∴
| FH |
| PF |
| CD |
| PC |
3
| ||
| 17 |
点评:本题考查直线与平面平行的证明,考查点F到平面PCE的距离的求法.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.