题目内容
 (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动,
(Ⅰ)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在边BC的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,二面角P-DE-A的大小为45°?
分析:(I)当点E为BC的中点时,由三角形中位线定理可得EF∥PC,进而由线面平行的判定定理可得EF∥平面PAC.
(II)由题意可得此题是证明线面垂直的问题,即证明直线AF垂直于平面PBE,而当点E在BC上无论怎样运动时直线PE都在此平面内,因此只需证明已知直线垂直于平面内的两条相交直线即可.
(III)过A作AG⊥DG于G,连PG,根据二面角的定义可得∠PAG是二面角P-DE-A的平面角,因为∠PGA=45°且PD与平面ABCD所成角是30°,所以∠PDA=30°,进而可得一些有关相等的长度,设BE=x,则GE=x,CE=3-x,利用△DCE是直角三角形.
(II)由题意可得此题是证明线面垂直的问题,即证明直线AF垂直于平面PBE,而当点E在BC上无论怎样运动时直线PE都在此平面内,因此只需证明已知直线垂直于平面内的两条相交直线即可.
(III)过A作AG⊥DG于G,连PG,根据二面角的定义可得∠PAG是二面角P-DE-A的平面角,因为∠PGA=45°且PD与平面ABCD所成角是30°,所以∠PDA=30°,进而可得一些有关相等的长度,设BE=x,则GE=x,CE=3-x,利用△DCE是直角三角形.
解答:解法一:
(Ⅰ)解:当点E为BC的中点时,EF与平面PAC平行
∵在△PBC中,E、F分别为BC、PB的中点…(1分)
∴EF∥PC
又EF?平面PAC,PC?平面PAC…(2分)
∴EF∥平面PAC…(3分)
(Ⅱ)证明:∵PA⊥平面ABCD,BE?平面ABCD
∴BE⊥PA
∵ABCD是矩形
∴BE⊥AB…(4分)
又AB∩AP=A,AP、AB?平面ABCD
∴BE⊥平面ABCD
又AF?平面PAB
∴AF⊥BE …(5分)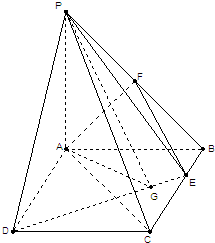
又PA=AB=1,且点F是PB的中点
∴PB⊥AF
又∵PB∩BE=B,PB、BE?平面PBE
∴AF⊥平面PBE …(6分)
∵PE?平面PBE
∴AF⊥PE
故无论点E在边BC的何处,都有PE⊥AF …(7分)
(Ⅲ)解:当BE=
-
时,二面角P-DE-A的大小为45°…(8分)
过A作AG⊥DE于G,连接PG
又∵DE⊥PA
∴DE⊥平面PAG∴DE⊥PG
则∠PGA是二面角P-DE-A的平面角∴∠PGA=45° …(10分)
∵PA⊥平面ABCD
∴∠PDA就是PD与平面ABCD所成的角,即∠PDA=30°…(11分)
又PA=AB=1,∴AD=
∴AG=1,DG=
…(12分)
设BE=x,则GE=x,CE=
-x
在Rt△DCE中,(
+x)2=(
-x)2+1
解得:x=
-
或x=
+
(舍去) …(13分)
故当BE=
-
时,二面角P-DE-A的大小为45°…(14分)
(Ⅰ)解:当点E为BC的中点时,EF与平面PAC平行
∵在△PBC中,E、F分别为BC、PB的中点…(1分)
∴EF∥PC
又EF?平面PAC,PC?平面PAC…(2分)
∴EF∥平面PAC…(3分)
(Ⅱ)证明:∵PA⊥平面ABCD,BE?平面ABCD
∴BE⊥PA
∵ABCD是矩形
∴BE⊥AB…(4分)
又AB∩AP=A,AP、AB?平面ABCD
∴BE⊥平面ABCD
又AF?平面PAB
∴AF⊥BE …(5分)

又PA=AB=1,且点F是PB的中点
∴PB⊥AF
又∵PB∩BE=B,PB、BE?平面PBE
∴AF⊥平面PBE …(6分)
∵PE?平面PBE
∴AF⊥PE
故无论点E在边BC的何处,都有PE⊥AF …(7分)
(Ⅲ)解:当BE=
| 3 |
| 2 |
过A作AG⊥DE于G,连接PG
又∵DE⊥PA
∴DE⊥平面PAG∴DE⊥PG
则∠PGA是二面角P-DE-A的平面角∴∠PGA=45° …(10分)
∵PA⊥平面ABCD
∴∠PDA就是PD与平面ABCD所成的角,即∠PDA=30°…(11分)
又PA=AB=1,∴AD=
| 3 |
| 2 |
设BE=x,则GE=x,CE=
| 3 |
在Rt△DCE中,(
| 2 |
| 3 |
解得:x=
| 3 |
| 2 |
| 3 |
| 2 |
故当BE=
| 3 |
| 2 |
点评:解决此类问题的关键是熟悉几何体的结构特征,得到有关线面垂直、线线垂直的结论,以及利用这些垂直关系解决二面角问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是
(2010•天津模拟)某几何体的三视图,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是