题目内容
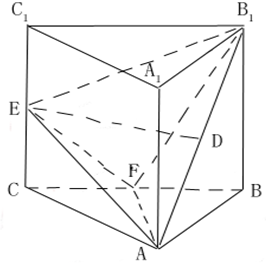 如图,已知直三棱柱ABC-A1B1C1中,△ABC是等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别是B1A、CC1、BC的中点.现设A1A=2a
如图,已知直三棱柱ABC-A1B1C1中,△ABC是等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别是B1A、CC1、BC的中点.现设A1A=2a(1)求证:DE∥平面ABC;
(2)求证:B1F⊥平面AEF;
(3)求二面角B1-AE-F的正切值.
分析:建立空间直角坐标系,求出相关向量
(I)要证:DE∥平面ABC,只需证明向量DE与平面ABC的法向量数量积=0即可;
(II)要证:B1F⊥平面AEF,只需证明
•
=(-2)×2+(-2)+(-4)×(-2)=0,
=(-2)×2+2×2+(-4)=0即可;
(III)求二面角B1-AE-F的余弦值,只需求出平面B1AE的法向量为
=(x,y,z),
平面AEF的法向量为
,利用数量积确定二面角的余弦值.
也可以用几何法证明:
(I)要证DE∥平面ABC,只需证明DE平行平面ABC内的直线DG(设G是AB的中点,连接DG,);
(II)求证B1F⊥平面AEF,只需证明B1F垂直平面AEF内的两条相交直线AF、EF即可;
(III)过F做FM⊥AE于点M,连接B1M,说明∠B1MF为二面角B1-AE-F的平面角,然后求二面角B1-AE-F的余弦值.
(I)要证:DE∥平面ABC,只需证明向量DE与平面ABC的法向量数量积=0即可;
(II)要证:B1F⊥平面AEF,只需证明
| B1F |
| EF |
| B1F• |
| AF |
(III)求二面角B1-AE-F的余弦值,只需求出平面B1AE的法向量为
| n |
平面AEF的法向量为
|
也可以用几何法证明:
(I)要证DE∥平面ABC,只需证明DE平行平面ABC内的直线DG(设G是AB的中点,连接DG,);
(II)求证B1F⊥平面AEF,只需证明B1F垂直平面AEF内的两条相交直线AF、EF即可;
(III)过F做FM⊥AE于点M,连接B1M,说明∠B1MF为二面角B1-AE-F的平面角,然后求二面角B1-AE-F的余弦值.
解答: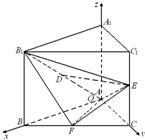 解:方法1:如图建立空间直角坐标系O-xyz,令AB=AA1=4,
解:方法1:如图建立空间直角坐标系O-xyz,令AB=AA1=4,
则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),
B1(4,0,4),D(2,0,2),(2分)
(I)
=(-2,4,0),面ABC的法向量为
=(0,0,4),
∵
•
=0,DE?平面ABC,
∴DE∥平面ABC.(4分)
(II)
=(-2,2,-4),
=(2,-2,-2)
•
=(-2)×2+(-2)+(-4)×(-2)=0
=(-2)×2+2×2+(-4)=0(6分)
∴
⊥
,∴B1F⊥AF
∵AF∩FE=F,∴B1F⊥平面AEF(8分)
(III)平面AEF的法向量为
,设平面B1AE的法向量为
=(x,y,z),
∴
,即
(10分)
令x=2,则Z=-2,y=1,∴
=(2,1,-2)
∴cos(
,
)=
=
=
∴二面角B1-AE-F的余弦值为
(12分)
方法2:(I)方法i:设G是AB的中点,连接DG,
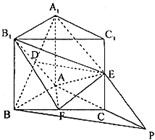 则DG平行且等于EC,(2分)
则DG平行且等于EC,(2分)
所以四边形DECG是平行四边形,所以DE∥GC,
从而DE∥平面ABC.(4分)
方法ii:连接A1B、A1E,并延长A1E交AC的延长线
于点P,连接BP.由E为C1C的中点,A1C1∥CP,
可证A1E=EP,(2分)
∵D、E是A1B、A1P的中点,∴DE∥BP,
又∵BP?平面ABC,DE?平面ABC,∴DE∥平面ABC(4分)
(II)∵△ABC为等腰直角三角形,F为BC的中点,
∴BC⊥AF,又∵B1B⊥平面ABC,可证B1F⊥AF,(6分)
设AB=AA1=2,则 B1F=
,EF=
,B1E=3
∴B1F⊥EF,∴B1F⊥平面AEF;(8分)
(III)过F做FM⊥AE于点M,连接B1M,
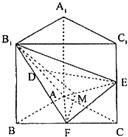 ∵B1F⊥平面AEF,由三垂线定理可证B1M⊥AE,
∵B1F⊥平面AEF,由三垂线定理可证B1M⊥AE,
∴∠B1MF为二面角B1-AE-F的平面角,
C1C⊥平面ABC,AF⊥FC,可证EF⊥AF,
在Rt△AEF中,可求 FM=
,(10分)
在Rt△B1FM中,∠B1FM=90°,∴cos∠B1MF=
∴二面角B1-AE-F的余弦值为
(12分)
 解:方法1:如图建立空间直角坐标系O-xyz,令AB=AA1=4,
解:方法1:如图建立空间直角坐标系O-xyz,令AB=AA1=4,则A(0,0,0),E(0,4,2),F(2,2,0),B(4,0,0),
B1(4,0,4),D(2,0,2),(2分)
(I)
| DE |
| OA1 |
∵
| DE |
| OA1 |
∴DE∥平面ABC.(4分)
(II)
| B1F |
| EF |
| B1F |
| EF |
| B1F• |
| AF |
∴
| B1F |
| AF |
∵AF∩FE=F,∴B1F⊥平面AEF(8分)
(III)平面AEF的法向量为
|
| n |
∴
|
|
令x=2,则Z=-2,y=1,∴
| n |
∴cos(
| n |
| B1F |
| ||||
|
|
| 6 | ||||
|
| ||
| 6 |
∴二面角B1-AE-F的余弦值为
| ||
| 6 |
方法2:(I)方法i:设G是AB的中点,连接DG,
 则DG平行且等于EC,(2分)
则DG平行且等于EC,(2分)所以四边形DECG是平行四边形,所以DE∥GC,
从而DE∥平面ABC.(4分)
方法ii:连接A1B、A1E,并延长A1E交AC的延长线
于点P,连接BP.由E为C1C的中点,A1C1∥CP,
可证A1E=EP,(2分)
∵D、E是A1B、A1P的中点,∴DE∥BP,
又∵BP?平面ABC,DE?平面ABC,∴DE∥平面ABC(4分)
(II)∵△ABC为等腰直角三角形,F为BC的中点,
∴BC⊥AF,又∵B1B⊥平面ABC,可证B1F⊥AF,(6分)
设AB=AA1=2,则 B1F=
| 6 |
| 3 |
∴B1F⊥EF,∴B1F⊥平面AEF;(8分)
(III)过F做FM⊥AE于点M,连接B1M,
 ∵B1F⊥平面AEF,由三垂线定理可证B1M⊥AE,
∵B1F⊥平面AEF,由三垂线定理可证B1M⊥AE,∴∠B1MF为二面角B1-AE-F的平面角,
C1C⊥平面ABC,AF⊥FC,可证EF⊥AF,
在Rt△AEF中,可求 FM=
| ||
| 5 |
在Rt△B1FM中,∠B1FM=90°,∴cos∠B1MF=
| ||
| 6 |
∴二面角B1-AE-F的余弦值为
| ||
| 6 |
点评:本题考查直线与平面平行的判定,二面角的求法,直线与平面的垂直的判定,考查逻辑思维能力 空间想象能力,是中档题.

练习册系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点. 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,E是棱CC1上动点,F是AB中点,AC=BC=2,AA1=4. 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点. 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. (2010•莒县模拟)如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CCl、AB中点.
(2010•莒县模拟)如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CCl、AB中点.