题目内容
已知点P是直角坐标平面内的动点,点P到直线l1:x=-2的距离为d1,到点F(-1,0)的距离为d2,且
=
.
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使
=λS1S3成立.若存在,求出λ的值;若不存在,请说明理由.
| d2 |
| d1 |
| ||
| 2 |
(1)求动点P所在曲线C的方程;
(2)直线l过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线l1:x=-2的垂线,对应的垂足分别为M、N,试判断点F与以线段MN为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
(3)记S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),问是否存在实数λ,使
| S | 2 2 |
分析:(1)设出P的坐标,利用已知条件列出方程求解求动点P所在曲线C的方程;
(2)利用直线l与椭圆的故选列出方程,求出两个坐标的关系,通过点与圆的位置关系,可以比较点到圆心的距离与半径的大小来判断,也可以计算点与直径形成的张角是锐角、直角、钝角来加以判断.
(3)利用弦长公式两点距离公式,求出S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),使
=λS1S3成立.求出λ的值即可.
(2)利用直线l与椭圆的故选列出方程,求出两个坐标的关系,通过点与圆的位置关系,可以比较点到圆心的距离与半径的大小来判断,也可以计算点与直径形成的张角是锐角、直角、钝角来加以判断.
(3)利用弦长公式两点距离公式,求出S1=S△FAM,S2=S△FMN,S3=S△FBN(A、B、M、N是(2)中的点),使
| S | 2 2 |
解答: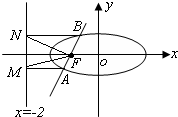 解 (1)设动点为P(x,y),依据题意,有
解 (1)设动点为P(x,y),依据题意,有
=
,化简得
+y2=1. …(3分)
因此,动点P所在曲线C的方程是:
+y2=1. …(4分)
(2)点F在以MN为直径的圆的外部.
理由:由题意可知,当过点F的直线l的斜率为0时,不合题意,故可设直线l:x=my-1,如图所示. (5分)
联立方程组
,可化为(2+m2)y2-2my-1=0,
则点A(x1,y1)、B(x2,y2)的坐标满足
. (7分)
又AM⊥l1、BN⊥l1,可得点M(-2,y1)、N(-2,y2).
因
=(-1,y1),
=(-1,y2),则
•
=(-1,y1)•(-1,y2)=1+y1y2=
>0.(9分)
于是,∠MFN为锐角,即点F在以MN为直径的圆的外部. (10分)
(3)依据(2)可算出x1+x2=m(y1+y2)-2=-
,x1x2=(my1-1)(my2-1)=
,
则 S1S3=
(x1+2)|y1|•
(x2+2)|y2|=
•
[x1x2+2(x1+x2)+4]=
,
=(
|y1-y2|•1)2=
[(y1+y2)2-4y1y2]=2
. (15分)
所以,
=4S1S3,即存在实数λ=4使得结论成立. (16分)
 解 (1)设动点为P(x,y),依据题意,有
解 (1)设动点为P(x,y),依据题意,有
| ||
| |x+2| |
| ||
| 2 |
| x2 |
| 2 |
因此,动点P所在曲线C的方程是:
| x2 |
| 2 |
(2)点F在以MN为直径的圆的外部.
理由:由题意可知,当过点F的直线l的斜率为0时,不合题意,故可设直线l:x=my-1,如图所示. (5分)
联立方程组
|
则点A(x1,y1)、B(x2,y2)的坐标满足
|
又AM⊥l1、BN⊥l1,可得点M(-2,y1)、N(-2,y2).
因
| FM |
| FN |
| FM |
| FN |
| 1+m2 |
| 2+m2 |
于是,∠MFN为锐角,即点F在以MN为直径的圆的外部. (10分)
(3)依据(2)可算出x1+x2=m(y1+y2)-2=-
| 4 |
| 2+m2 |
| 2-2m2 |
| 2+m2 |
则 S1S3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2+m2 |
| 1 |
| 2 |
| 1+m2 |
| (2+m2)2 |
| S | 2 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1+m2 |
| (2+m2)2 |
所以,
| S | 2 2 |
点评:本题考查椭圆方程的求法,直线与椭圆的位置关系与直线与圆的位置关系的判断,三角形的面积公式的应用,向量数量积的应用,考查计算能力,转化思想.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
 的距离为d1,到点F(–
1,0)的距离为d2,且
的距离为d1,到点F(–
1,0)的距离为d2,且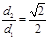 .
. 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为 ,试判断点F与以线段
,试判断点F与以线段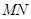 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况); ,
, ,
, (A、B、
(A、B、 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数 ,使
,使 成立.若存在,求出
成立.若存在,求出