题目内容
已知点P是直角坐标平面内的动点,点P到直线x=-
-1(p是正常数)的距离为d1,到点F(
,0)的距离为d2,且d1-d2=1.
(1)求动点p所在曲线C的方程
(2)直线l过点F且与曲线C交于不同两点A、B,分别过A、B点作直线l1:x=-
的垂线,对应的垂足分别为M、N,求证:FM⊥FN.
| p |
| 2 |
| p |
| 2 |
(1)求动点p所在曲线C的方程
(2)直线l过点F且与曲线C交于不同两点A、B,分别过A、B点作直线l1:x=-
| p |
| 2 |
分析:(1)设动点为P(x,y),利用d1-d2=1,可得方程,化简可得结论;
(2)设直线l的方程与抛物线联立,利用韦达定理及向量的数量积,可得结论.
(2)设直线l的方程与抛物线联立,利用韦达定理及向量的数量积,可得结论.
解答:(1)解:设动点为P(x,y),(1分)
依据题意,有|x+
+1|-
=1,化简得y2=2px. (4分)
因此,动点P所在曲线C的方程是:y2=2px. …(6分)
(2)证明:由题意可知,当过点F的直线l的斜率为0时,不合题意,故可设直线l:x=my+
. (8分)
联立方程组
,可化为y2-2mpy-p2=0,
则点A(x1,y1)、B(x2,y2)的坐标满足
. (10分)
又AM⊥l1、BN⊥l1,可得点M(-
,y1)、N(-
,y2).
于是,
=(-p,y1),
=(-p,y2),
因此
•
=(-p,y1)•(-p,y2)=p2+y1y2=0. (12分)
依据题意,有|x+
| p |
| 2 |
(x-
|
因此,动点P所在曲线C的方程是:y2=2px. …(6分)
(2)证明:由题意可知,当过点F的直线l的斜率为0时,不合题意,故可设直线l:x=my+
| p |
| 2 |
联立方程组
|
则点A(x1,y1)、B(x2,y2)的坐标满足
|
又AM⊥l1、BN⊥l1,可得点M(-
| p |
| 2 |
| p |
| 2 |
于是,
| FM |
| FN |
因此
| FM |
| FN |
点评:本题考查轨迹方程的求法及直线与椭圆的相关知识,考查直线与圆锥曲线的综合应用能力,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 的距离为d1,到点F(–
1,0)的距离为d2,且
的距离为d1,到点F(–
1,0)的距离为d2,且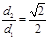 .
. 过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线
过点F且与曲线C交于不同两点A、B(点A或B不在x轴上),分别过A、B点作直线 的垂线,对应的垂足分别为
的垂线,对应的垂足分别为 ,试判断点F与以线段
,试判断点F与以线段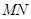 为直径的圆的位置关系(指在圆内、圆上、圆外等情况);
为直径的圆的位置关系(指在圆内、圆上、圆外等情况); ,
, ,
, (A、B、
(A、B、 是(2)中的点),问是否存在实数
是(2)中的点),问是否存在实数 ,使
,使 成立.若存在,求出
成立.若存在,求出