题目内容
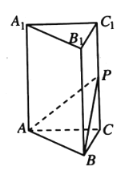
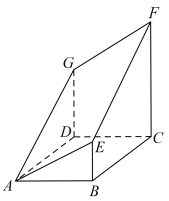
【题目】如图所示,多面体是由底面为![]() 的直四棱柱被截面
的直四棱柱被截面![]() 所截而得到的,该直四棱柱的底面为菱形,其中
所截而得到的,该直四棱柱的底面为菱形,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)求平面![]() 与底面
与底面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1) ![]() ;(2)
;(2)![]()
【解析】
(1)由面面平行的性质定理可知,四边形![]() 为平行四边形,以菱形对角线的交点为原点建立空间直角坐标系,写出各点坐标,求出向量
为平行四边形,以菱形对角线的交点为原点建立空间直角坐标系,写出各点坐标,求出向量![]() 坐标,再求
坐标,再求![]() 即可;
即可;
(2)分别求出平面![]() 与底面
与底面![]() 的法向量,利用向量的夹角公式求出法向量的夹角余弦值,进而可求出平面
的法向量,利用向量的夹角公式求出法向量的夹角余弦值,进而可求出平面![]() 与底面
与底面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
因为多面体是由底面为![]() 的直四棱柱被截面
的直四棱柱被截面![]() 所截而得到的,
所截而得到的,
所以平面![]()
![]() 平面
平面![]() ,又平面
,又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() ,同理
,同理![]() ,所以四边形
,所以四边形![]() 是平行四边形,
是平行四边形,
连结![]() ,
,![]() 交于
交于![]() ,以
,以![]() 为原点,
为原点,![]() 所在直线分别为
所在直线分别为![]() 轴,
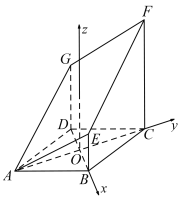
轴,![]() 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() 的长为
的长为![]() .
.
(2)根据题意可取平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由(1)知![]() ,
,![]() ,设平面
,设平面![]() 的法向量为
的法向量为![]() ,则
,则
由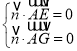 ,得
,得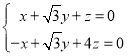 ,即
,即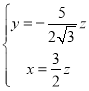 ,
,
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以平面![]() 与底面
与底面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】已知某次考试之后,班主任从全班同学中随机抽取一个容量为8的样本,他们的数学、物理成绩(单位:分)对应如下表,对应散点图如图所示:
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学成绩 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理成绩 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
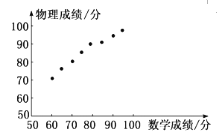
根据以上信息,则下列结论:
①根据散点图,可以判断数学成绩与物理成绩具有线性相关关系;
②根据散点图,可以判断数学成绩与物理成绩具有一次函数关系;
③从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则可以判断出甲同学的物理成绩一定比乙同学的物理成绩高;
④从全班随机抽取2名同学(记为甲、乙),若甲同学的数学成绩为80分,乙同学的数学成绩为60分,则不能判断出甲同学的物理成绩一定比乙同学的物理成绩高;
其中正确的个数是( )
A.1B.2C.3D.4