题目内容
【题目】如图，
为圆锥的顶点，
是圆锥底面的圆心，
是底面的内接正三角形，
为
上一点，∠APC=90°．
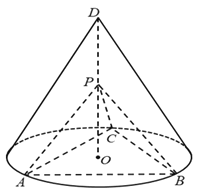
（1）证明：平面PAB⊥平面PAC；
（2）设DO=
，圆锥的侧面积为
，求三棱锥PABC的体积.
【答案】（1）证明见解析；（2）
.
【解析】
（1）根据已知可得
，进而有
≌
，可得
，即
，从而证得
平面
，即可证得结论；
（2）将已知条件转化为母线
和底面半径
的关系，进而求出底面半径，由正弦定理，求出正三角形
边长，在等腰直角三角形
中求出
，在
中，求出
，即可求出结论.
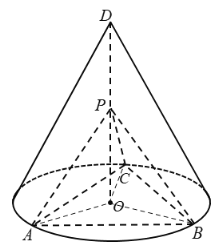
（1）连接
，
为圆锥顶点，
为底面圆心，
平面，
在
上，
，
是圆内接正三角形，
，≌，
，即
，
平面
平面
，
平面
平面；
（2）设圆锥的母线为，底面半径为，圆锥的侧面积为
，
，解得
，
，
在等腰直角三角形中，
，
在
中，
，
三棱锥
的体积为
.
练习册系列答案
相关题目
