题目内容
如图所示,在四棱锥 中,底面
中,底面 为矩
为矩
形, ⊥平面
⊥平面 ,
, ,
, 为
为 上的点,若
上的点,若 ⊥平面
⊥平面

(1)求证: 为
为 的中点;
的中点;
(2)求二面角 的大小.
的大小.
 中,底面
中,底面 为矩
为矩形,
 ⊥平面
⊥平面 ,
, ,
, 为
为 上的点,若
上的点,若 ⊥平面
⊥平面

(1)求证:
 为
为 的中点;
的中点;(2)求二面角
 的大小.
的大小.(1)由PD⊥平面MAB, 平面MAB,则PD⊥MA,同时PA=AD,进而得到证明。
平面MAB,则PD⊥MA,同时PA=AD,进而得到证明。
(2)120°
 平面MAB,则PD⊥MA,同时PA=AD,进而得到证明。
平面MAB,则PD⊥MA,同时PA=AD,进而得到证明。(2)120°
试题分析:解:(1)由PD⊥平面MAB,
 平面MAB,则PD⊥MA 2分
平面MAB,则PD⊥MA 2分又PA=AD,则△APM≌△AMD,因而PM=DM,即M为PD的中点; 5分
(2)以A原点,以
 所在直线分别为x轴、y轴、z轴建立空间直角坐标系,
所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则A(0,0,0),B(1,0,0),C(1,2,0),D(0,2,0),P(0,0,2),M(0,1,1),
由(1)知
 =(0,-1,1)为平面MAB的法向量, 7分
=(0,-1,1)为平面MAB的法向量, 7分设平面MBC的法向量
 =(x,y,z),
=(x,y,z), =(1,1,-1),
=(1,1,-1), = (0,2,0),
= (0,2,0),
 =0,
=0, 
 =0,即
=0,即 ,令x=z=1,则
,令x=z=1,则 =(1,0,1), 10分
=(1,0,1), 10分 , 11分
, 11分而二面角A—BM—C为钝角,因而其大小为120°. 12分
点评:解决的关键是利用空间向量结合向量的数量积来表示角的大小,属于基础题。

练习册系列答案
相关题目
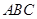 —
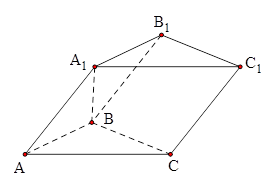
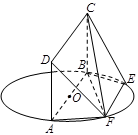
—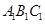 ,侧面
,侧面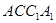 与底面
与底面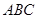 垂直,∠
垂直,∠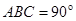 ,
,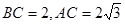 ,且
,且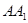 ⊥
⊥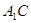 ,
,
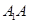 与平面
与平面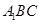 是否垂直,并说明理由;
是否垂直,并说明理由;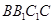 与底面
与底面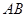 为圆
为圆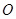 的直径,点
的直径,点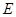 、
、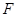 在圆
在圆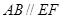 ,矩形
,矩形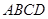 所在的平面与圆
所在的平面与圆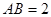 ,
,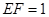 .
.
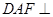 平面
平面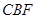 ;
;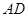 的长为何值时,平面
的长为何值时,平面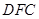 与平面
与平面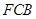 所成的锐二面角的大小为
所成的锐二面角的大小为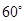 ?
?
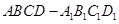 中,下底
中,下底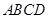 是边长为
是边长为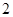 的正方形,上底
的正方形,上底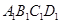 是边长为1的正方形,侧棱
是边长为1的正方形,侧棱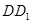 ⊥平面
⊥平面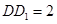 .
.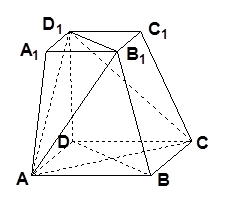
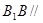 平面
平面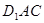 ;
;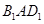 与平面
与平面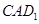 夹角的余弦值.
夹角的余弦值.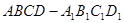 中,
中, 是棱
是棱 的中点.
的中点.
 平面
平面 ;
; .
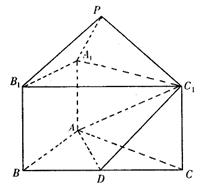
.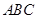 为正三角形的直三棱柱
为正三角形的直三棱柱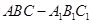 中,
中,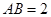 ,
,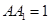 ,
,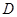 是
是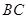 的中点,点
的中点,点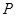 在平面
在平面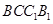 内,
内,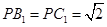 .
. 
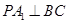 ;
; 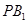 ∥平面
∥平面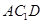 ;
;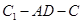 的大小.
的大小.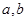 为两条直线,
为两条直线,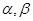 为两个平面,则下列结论成立的是( )
为两个平面,则下列结论成立的是( ) 且
且 ,则
,则
 ,则
,则
 ,
, 则
则 则
则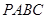 的六条边均相等,
的六条边均相等, 分别是
分别是 的中点,则下列四个结论中不成立的是 ( )
的中点,则下列四个结论中不成立的是 ( ) 
 平面
平面
 平面
平面
 //平面
//平面
 平面
平面