题目内容
（2004•朝阳区一模）已知a=
(
+
+…+
)，b=
(1+
+
+…+
+…)，则a、b的值分别为
，
，
，c=
=
．
| lim |
| n→+∞ |
| 1 |
| n2 |
| 2 |
| n2 |
| n |
| n2 |
| lim |
| n→+∞ |
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3n-1 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| lim |
| n→+∞ |
| an+bn |
| an+1+bn+1 |
| 2 |
| 3 |
| 2 |
| 3 |
分析：先利用等差、等比数列的前n项和公式对a，b进行化简，然后再求极限可得a，b，把a，b值代入c化简后可求得极限．
解答：解：∵
+
+…+
=
=
，∴a=
=
=
；
∵1+
+
+…+
=
，∴b=
=
；
则
=
=
，
所以c=
=
，
故答案为：
，
；
．
| 1 |
| n2 |
| 2 |
| n2 |
| n |
| n2 |
| ||
| n2 |
| n+1 |
| 2n |
| lim |
| n→∞ |
| n+1 |
| 2n |
| lim |
| n→∞ |
1+
| ||
| 2 |
| 1 |
| 2 |
∵1+
| 1 |
| 3 |
| 1 |
| 9 |
| 1 |
| 3n-1 |
1-
| ||
1-
|
| lim |
| n→∞ |
1-
| ||
1-
|
| 3 |
| 2 |
则
| an+bn |
| an+1+bn+1 |
| ||||
|
| ||||||
|
所以c=
| lim |
| n→∞ |
| ||||||
|
| 2 |
| 3 |
故答案为：
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
点评：本题考查等差、等比数列的前n项和公式、数列极限及其运算，考查学生的运算能力．
练习册系列答案
相关题目
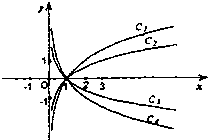（2004•朝阳区一模）已知图中曲线C1、C2、C3、C4是函数logax的图象，则曲线C1、C2、C3、C4对应的a的值依次为（ ）