题目内容
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如图所示.
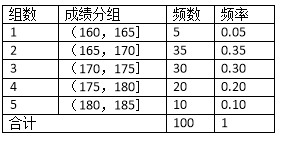
(1)为了能选拔出最优秀的学生,该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试,求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(2)在(1)的前提下,学校决定在6名学生中随机抽取2名学生接受A考官的面试,求第四组至少有一名学生被考官A面试的概率?
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)用分层抽样的方法获取样本中的比例;(2)用列举的方法得到从![]() 名学生中随机抽取
名学生中随机抽取![]() 名学生的所有结果数为
名学生的所有结果数为![]() 个,第四组至少有一名学生被面试的结果数为
个,第四组至少有一名学生被面试的结果数为![]() 个,由古典概型
个,由古典概型![]() .
.
试题解析:解:(1)6×![]() =3,6×
=3,6×![]() =2,6×
=2,6×![]() =1.
=1.
故第3、4、5组每组各抽取3,2,1名学生进入第二轮面试.
(2)设第3、4、5组抽取的学生分别为:a,b,c,1,2,m.则其所有的基本事件有:
(a,b),(a,c),(a,1),(a,2),(a,m),(b,c),(b,1),(b,2),(b,m),
(c,1),(c,2),(c,m),(1,2),(1,m),(2,m).共有15个
设事件B表示第四组至少有一名学生被考官A面试,其包含的基本事件有:(a,1),(a,2),(b,1),(b,2),(c,1),(c,2),(1,2),(1,m),(2,m)共9个;
∴![]()
![]() =0.6
=0.6
答:第四组至少有一名学生被考官A面试的概率为0.6

【题目】为了判断高中三年级学生选修文理科是否与性别有关,现随机抽取50名学生,得到2×2列联表:
理科 | 文科 | 总计 | |
男 | 13 | 10 | 23 |
女 | 7 | 20 | 27 |
总计 | 20 | 30 | 50 |
已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.根据表中数据,得到K2≈4.844,则认为选修文理科与性别有关系出错的可能性约为________.