题目内容
已知等差数列{ an }的公差为d(d≠0),且a3+ a 6+ a 10+ a 13=32,若am=8,则m为( )
| A.12 | B.8 | C.6 | D.4 |
B
解析试题分析:解:由等差中项的性质可得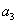 +
+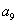 +
+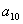 +
+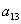 =32=4
=32=4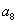 ,故
,故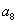 =8,则m=8,故选B.
=8,则m=8,故选B.
考点:等差数列
点评:根据等差数列的中项性质来化简,是解决该试题的关键,属于基础题。

练习册系列答案
相关题目
已知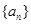 为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为
为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为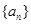 的前n项和(
的前n项和( N*),则S10的值为 ( )
N*),则S10的值为 ( )
| A.-110 | B.-90 | C.90 | D.110 |
等差数列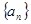 中,若
中,若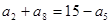 ,则
,则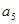 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
古希腊人常用小石子在沙滩上摆成各种形状来研究数。比如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似的,称图2中的1,4,9,16,…这样的数为正方形数。下列数中既是三角形数又是正方形数的是( )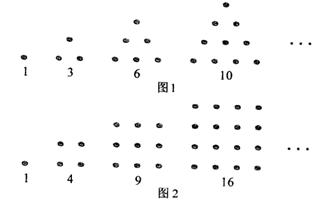
| A.289 | B.1225 | C.1024 | D.1378 |
设Sn是等差数列{an}的前n项和,若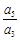 =
=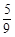 ,则
,则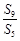 =( ).
=( ).
| A.1 | B.-1 | C.2 | D.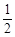 |
已知数列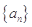 满足
满足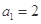 ,
,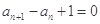
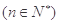 ,则此数列的通项
,则此数列的通项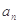 等于( )
等于( )
A.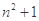 | B.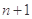 | C.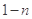 | D.3-n |
等差数列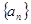 的前项
的前项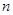 和为
和为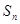 ,若
,若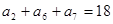 ,则
,则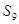 的值为( )
的值为( )
A.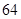 | B.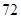 | C.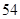 | D.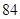 |
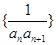 的前100项和为( )
的前100项和为( )