题目内容
已知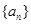 为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为
为等差数列,其公差为-2,且a7是a3与a9的等比中项,Sn为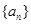 的前n项和(
的前n项和( N*),则S10的值为 ( )
N*),则S10的值为 ( )
| A.-110 | B.-90 | C.90 | D.110 |
D
解析试题分析:因为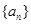 为等差数列,其公差为-2,所以a3=a7-4d= a7+8, a9=a7+2d= a7-4,又a7是a3与a9的等比中项,所以a7=8,a1=20,S10的值,10 a1
为等差数列,其公差为-2,所以a3=a7-4d= a7+8, a9=a7+2d= a7-4,又a7是a3与a9的等比中项,所以a7=8,a1=20,S10的值,10 a1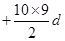 =110,故选D。
=110,故选D。
考点:本题主要考查等差数列的通项公式、求和公式以及等比中项的概念。
点评:小综合题,本题综合考查差数列的通项公式、求和公式以及等比中项的概念,解题思路比较明确,先通过a7是a3与a9的等比中项,确定等差数列项的关系。

练习册系列答案
相关题目
公差不为零的等差数列第2,3,6项构成等比数列,则这三项的公比为( )
| A.1 | B.2 | C.3 | D.4 |
设等差数列 的前
的前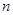 项和为
项和为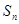 ,已知
,已知 ,
,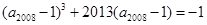 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.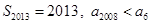 | B.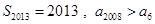 |
C.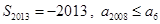 | D.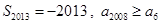 |
在等差数列 中,
中, +
+ =10则
=10则 的值为
的值为
| A.5 | B.6 | C.8 | D. 10 |
在等差数列 中,若
中,若 ,则
,则 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
公差不为零的等差数列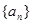 中,
中, ,数列
,数列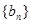 是等比数列,且
是等比数列,且  ( )
( )
| A.2 | B.4 | C.8 | D.16 |
若数列{an}是公差为 的等差数列,它的前100项和为145,则a1+a3+a5+…+a99的值是
的等差数列,它的前100项和为145,则a1+a3+a5+…+a99的值是
| A.60 | B.72.5 | C.85 | D.120 |
已知等差数列{ an }的公差为d(d≠0),且a3+ a 6+ a 10+ a 13=32,若am=8,则m为( )
| A.12 | B.8 | C.6 | D.4 |
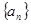 的前n项和为
的前n项和为 ,下列选项不可能是
,下列选项不可能是 的图像的是
的图像的是