题目内容
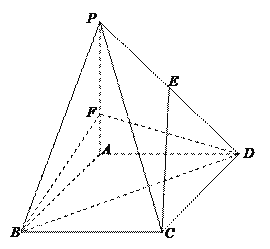
【题目】如图，在边长为3的菱形ABCD中，∠ABC=60°，
平面ABCD，且
，E为PD中点，F在棱PA上，且
.
（1）求证：CE∥平面BDF；
（2）求点P到平面BDF的距离.
【答案】（1）见解析;（2）
.
【解析】试题分析：
(1)利用题意取PF中点G，连接AC交BD于O点，连接FO，GC，EG
由题意易知平面EGC∥平面BDF， 
，∴CE∥平面BDF
(2)由题意利用体积相等，在四面体FABD中，易求得
， 
，∴P到平面BDF的距离等于
试题解析：
（1）
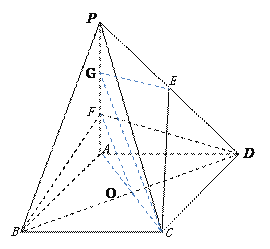
取PF中点G，连接AC交BD于O点，连接FO，GC，EG
由题意易知G为PF中点，又E为PD中点，所以GE∥FD，故
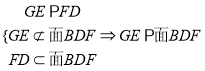
FO为三角形AGC的中位线，所以FO∥GC
所以面EGC∥平面BDF， 
，∴CE∥平面BDF
（2）由题意知点P到平面BDF的距离等于A到平面BDF的距离的两倍，记A到平面BDF的距离为h，则在四面体FABD中，易求得
由体积自等得
，
∴
，∴P到平面BDF的距离等于
练习册系列答案
相关题目
