题目内容
【题目】已知圆![]() ,圆
,圆![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的圆的切线为
的圆的切线为![]() 是圆上异于
是圆上异于![]() 的一点,
的一点,![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 是
是![]() 的中点,延长
的中点,延长![]() 分别交
分别交![]() 于
于![]() .
.

(1)若点![]() ,求以
,求以![]() 为直径的圆的方程,并判断
为直径的圆的方程,并判断![]() 是否在圆上;
是否在圆上;
(2)当![]() 在圆上运动时,证明:直线
在圆上运动时,证明:直线![]() 恒与圆
恒与圆![]() 相切.
相切.
【答案】(1)圆的方程为![]() ,且
,且![]() 在圆上;(2)证明见解析.
在圆上;(2)证明见解析.
【解析】试题分析:(1)已知点![]() 、
、![]() 的坐标,可求出直线
的坐标,可求出直线![]() 的方程,可求出点
的方程,可求出点![]() 的坐标,由圆的方程可知点
的坐标,由圆的方程可知点![]() 的坐标,可求出以
的坐标,可求出以![]() 为直径的圆的方程,将点
为直径的圆的方程,将点![]() 的坐标代入圆的方程,得在圆上;(2)要证明结论,需证明
的坐标代入圆的方程,得在圆上;(2)要证明结论,需证明![]() ,可先设点
,可先设点![]() 坐标,可求点
坐标,可求点![]() 坐标,进而可求点
坐标,进而可求点![]() 坐标,得
坐标,得![]() 与
与![]() 斜率,得
斜率,得![]() 得结论.
得结论.
试题解析:(1)由![]() ,∴直线
,∴直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,由
,由![]() ,
,![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ,∴
,∴![]() 为线段
为线段![]() 的中点,以
的中点,以![]() 为直径的圆恰以
为直径的圆恰以![]() 为圆心,半径等于
为圆心,半径等于![]() ,
,
所以,所求圆的方程为![]() ,且
,且![]() 在圆上,
在圆上,
(2)设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
在此方程中令![]() ,得
,得![]() ,
,
直线![]() 的斜率
的斜率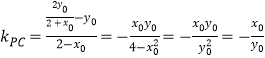 ,
,
若![]() ,则此时
,则此时![]() 与
与![]() 轴垂直,即
轴垂直,即![]() ,若
,若![]() ,则此时直线
,则此时直线![]() 的斜率为
的斜率为![]()
∴![]() ,即
,即![]() ,则直线
,则直线![]() 与圆
与圆![]() 相切
相切

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
【题目】某研究型学习小组调查研究学生使用智能手机对学习的影响.部分统计数据如下表:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
合计 | 20 | 10 | 30 |
附表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
经计算![]() ,则下列选项正确的是( )
,则下列选项正确的是( )
A.有99.5%的把握认为使用智能手机对学习有影响
B.有99.5%的把握认为使用智能手机对学习无影响
C.有99.9%的把握认为使用智能手机对学习有影响
D.有99.9%的把握认为使用智能手机对学习无影响