题目内容
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD是边长为 
的正方形，E为PC的中点，PB=PD．平面PBD⊥平面ABCD． 
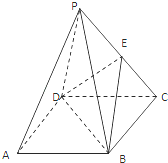
（1）证明：PA∥平面EDB．
（2）求三棱锥E﹣BCD与三棱锥P﹣ABD的体积比．
【答案】
（1）证明：连A、C交BD于O，连O、E，因为底面是正方形，所以，O是AC的中点，
又因为E是PC的中点，所以OE是△PAC的中位线，所以，OE∥PA，
又因为OE平面DEB，PA平面DEB，所以PA∥平面DEB．
（2）因为E是PC的中点，所以，E到平面ABCD的距离是P到平面ABCD的距离的一半，△BCD与△ABD的面积相等，
所以， ．
【解析】分析：（1）连A、C交BD于O，则OE是△PAC的中位线，可得OE∥PA，从而证明PA∥平面DEB．（2）E到平面ABCD的距离是P到平面ABCD的距离的一半，△BCD与△ABD的面积相等，故体积之比等于 
．
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行，以及对平面与平面垂直的性质的理解，了解两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直．
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求，剩余商品全部退回，则每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元.
（Ⅰ）若商店一天购进该商品10件,求当天的利润y（单位:元）关于当天需求量n（单位:件,n∈N）的函数解析式；
（Ⅱ）商店记录了50天该商品的日需求量（单位:件）,整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润（单位:元）的平均数；
②若该店一天购进10件该商品,记“当天的利润在区间
”为事件A，求P（A）的估计值.
【题目】“真人秀”热潮在我国愈演愈烈，为了了解学生是否喜欢某“真人秀”节目，在某中学随机调查了110名学生，得到如下列联表：
男 | 女 | 总计 | |
喜欢 | 40 | 20 | 60 |
不喜欢 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由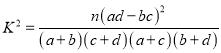
算得
.
附表：
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表，得到的正确结论是（ ）
A. 在犯错误的概率不超过
的前提下，认为“喜欢该节目与性别有关”
B. 在犯错误的概率不超过
的前提下，认为“喜欢该节目与性别无关”
C. 有
以上的把握认为“喜欢该节目与性别有关”
D. 有
【题目】微信已成为人们常用的社交软件，“微信运动”是微信里由腾讯开发的一个类似计步数据库的公众账号.手机用户可以通过关注“微信运动”公众号查看自己每天行走的步数，同时也可以和好友进行运动量的
或点赞.现从小明的微信朋友圈内随机选取了40人（男、女各20人），记录了他们某一天的走路步数，并将数据整理如下表：
步数 性别 | 0 | 2001 | 5001 | 8001 | ＞10000 |
男 | 1 | 2 | 4 | 7 | 6 |
女 | 0 | 3 | 9 | 6 | 2 |
若某人一天的走路步数超过8000步被系统评定为“积极型”，否则被系统评定为“懈怠型”.
（1）利用样本估计总体的思想，试估计小明的所有微信好友中每日走路步数超过10000步的概率；
（2）根据题意完成下面的
列联表，并据此判断能否有90%的把握认为“评定类型”与“性别”有关？
积极型 | 懈怠型 | 总计 | |
男 | |||
女 | |||
总计 |
附：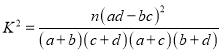 
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
