题目内容
已知函数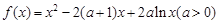 .
.
(Ⅰ)求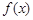 的单调区间;
的单调区间;
(Ⅱ)若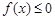 在区间
在区间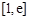 上恒成立,求实数
上恒成立,求实数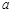 的取值范围.
的取值范围.
(Ⅰ)当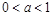 时,
时,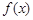 的单调增区间是
的单调增区间是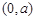 和
和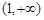 ,单调减区间是
,单调减区间是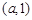 ;当
;当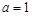 时,
时,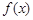 在
在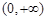 单调递增;当
单调递增;当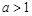 时,
时,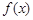 的单调增区间是
的单调增区间是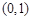 和
和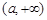 ,单调减区间是
,单调减区间是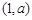 .
.
(Ⅱ)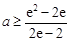 .
.
解析试题分析:(Ⅰ)首先求出导数,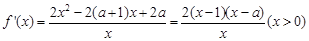 .由于含有参数
.由于含有参数 ,故分情况讨论. 利用
,故分情况讨论. 利用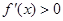 求得其递增区间,
求得其递增区间,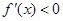 求得其递减区间.
求得其递减区间.
(Ⅱ)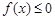 在区间
在区间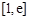 上恒成立,则
上恒成立,则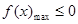 .由(1)可知
.由(1)可知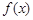 在区间
在区间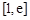 上只可能有极小值点,所以
上只可能有极小值点,所以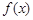 在区间
在区间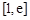 上的最大值在区间的端点处取到,求出端点的函数值比较大小,较大者即为最大值,然后由
上的最大值在区间的端点处取到,求出端点的函数值比较大小,较大者即为最大值,然后由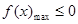 便可求出
便可求出 的范围.
的范围.
试题解析:(Ⅰ)求导得: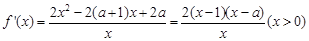 .
.
由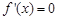 得
得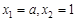 ,
,
当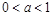 时,在
时,在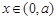 或
或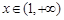 时
时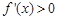 ,在
,在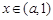 时
时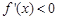 ,
,
所以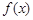 的单调增区间是
的单调增区间是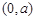 和
和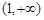 ,单调减区间是
,单调减区间是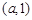 ;
;
当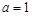 时,在
时,在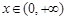 时
时 ,所以
,所以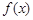 的单调增区间是
的单调增区间是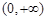 ;
;
当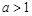 时,在
时,在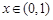 或
或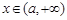 时
时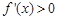 ,在
,在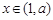 时
时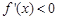 .
.
所以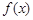 的单调增区间是
的单调增区间是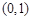 和
和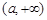 ,单调减区间是
,单调减区间是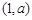 .
.
(Ⅱ)由(1)可知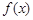 在区间
在区间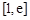 上只可能有极小值点,
上只可能有极小值点,
所以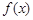 在区间
在区间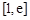 上的最大值在区间的端点处取到,
上的最大值在区间的端点处取到,
即有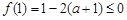 且
且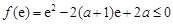 ,
,
解得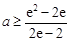 .
.
考点:1、导数的应用;2、不等关系.

练习册系列答案
相关题目
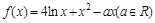 .
.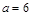 时,求函数
时,求函数 的单调区间;
的单调区间;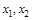 ,且
,且 ,求证:
,求证: ;
;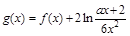 ,对于任意
,对于任意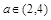 时,总存在
时,总存在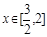 ,使
,使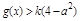 成立,求实数
成立,求实数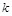 的取值范围.
的取值范围. ,
,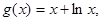 其中
其中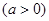
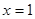 是函数
是函数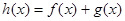 的极值点,求实数
的极值点,求实数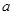 的值;
的值;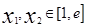 (
(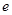 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数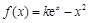 (其中
(其中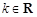 ,e是自然对数的底数).
,e是自然对数的底数).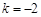 ,试判断函数
,试判断函数 在区间
在区间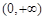 上的单调性;
上的单调性;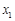 ,
,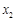 (
(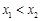 ),求k的取值范围;
),求k的取值范围;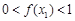 .
. (
( 为自然对数的底数)。
为自然对数的底数)。 ,求函数
,求函数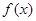 的单调区间;
的单调区间; ,使函数
,使函数 上是单调增函数?若存在,求出
上是单调增函数?若存在,求出
 ,又
,又 ,
,
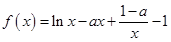 .
.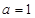 时,求曲线
时,求曲线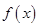 在
在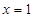 处的切线方程;
处的切线方程;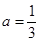 时,求函数
时,求函数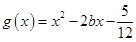 ,若对于
,若对于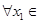 [1,2],
[1,2],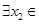 [0,1],使
[0,1],使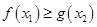 成立,求实数
成立,求实数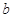 的取值范围.
的取值范围.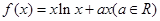 .
.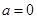 ,求
,求 的最小值;
的最小值;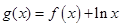 在区间
在区间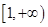 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;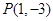 恰好能作函数
恰好能作函数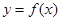 图象的两条切线,并且两切线的倾斜角互补,求实数
图象的两条切线,并且两切线的倾斜角互补,求实数 个月顾客对某种商品的需求总量
个月顾客对某种商品的需求总量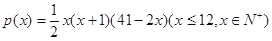 (单位:件)
(单位:件)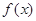 的表达式;
的表达式;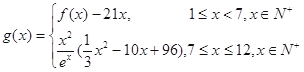 (单位:件),每件利润
(单位:件),每件利润 (单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据:
(单位:元),求该商场销售该商品,预计第几个月的月利润达到最大值?月利润的最大值是多少?(参考数据: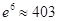 )
)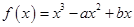 的图象与直线
的图象与直线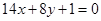 相切于点
相切于点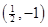 .
. 和
和 的值; (2)求
的值; (2)求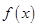 的极值.
的极值.