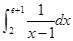题目内容
设函数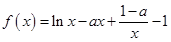 .
.
(1)当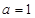 时,求曲线
时,求曲线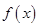 在
在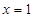 处的切线方程;
处的切线方程;
(2)当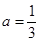 时,求函数
时,求函数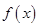 的单调区间;
的单调区间;
(3)在(2)的条件下,设函数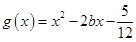 ,若对于
,若对于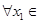 [1,2],
[1,2],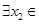 [0,1],使
[0,1],使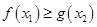 成立,求实数
成立,求实数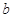 的取值范围.
的取值范围.
(1)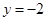 ;(2)单调增区间为
;(2)单调增区间为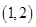 ;单调减区间为
;单调减区间为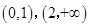 ;(3)b的取值范围是
;(3)b的取值范围是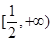
解析试题分析:(1)由函数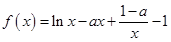 当
当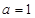 时,首先求出函数的定义域.再通过求导再求出导函数当
时,首先求出函数的定义域.再通过求导再求出导函数当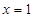 时的导函数的的值即为切线的斜率.又因为过点
时的导函数的的值即为切线的斜率.又因为过点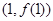 则可求出在
则可求出在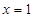 的切线方程.本小题主要考查对数的求导问题.
的切线方程.本小题主要考查对数的求导问题.
(2)当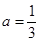 时通过求导即可得,再求出导函数的值为零时的x值.由于定义域是x大于零.所以可以根据导函数的正负值判断函数的单调性.
时通过求导即可得,再求出导函数的值为零时的x值.由于定义域是x大于零.所以可以根据导函数的正负值判断函数的单调性.
(3)由于在(2)的条件下,设函数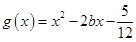 ,若对于
,若对于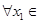 [1,2],
[1,2],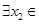 [0,1],使
[0,1],使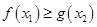 成立.等价于
成立.等价于 在
在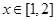 上的最小值要大于或等于
上的最小值要大于或等于 在
在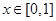 上的最小值.由于
上的最小值.由于 是递增的所以易求出最小值.再对
是递增的所以易求出最小值.再对 中的b进行讨论从而得到要求的结论.
中的b进行讨论从而得到要求的结论.
试题解析:函数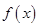 的定义域为
的定义域为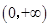 , 1分
, 1分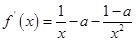 2分
2分
(1)当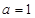 时,
时,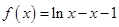 ,
,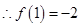 , 3分
, 3分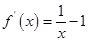 ,
,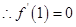 , 4分
, 4分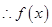 在
在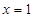 处的切线方程为
处的切线方程为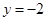 . 5分
. 5分
(2)  .
.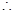 当
当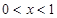 ,或
,或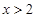 时,
时, 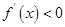 ; 6分
; 6分
当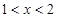 时,
时, 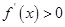 . 7分
. 7分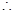 当
当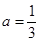 时,函数
时,函数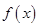 的单调增区间为
的单调增区间为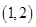 ;单调减区间为
;单调减区间为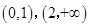 . 8分
. 8分
(如果把单调减区间写为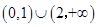 ,该步骤不得分)
,该步骤不得分)
(3)当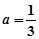 时,由(2)可知函数
时,由(2)可知函数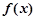 在
在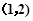 上为增函数,
上为增函数,
∴函数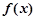 在[1,2]上的最小值为
在[1,2]上的最小值为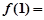
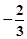 9分
9分
若对于 [1,2],
[1,2],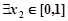
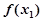 ≥
≥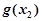 成立
成立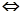
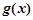 在
在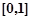 上的最小值不大于
上的最小值不大于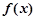 在[1,2]上的最小值(*)
在[1,2]上的最小值(*)

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案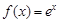 ,
,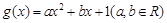 .
.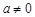 ,则
,则 ,
,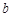 满足什么条件时,曲线
满足什么条件时,曲线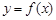 与
与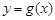 在
在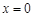 处总有相同的切线?
处总有相同的切线?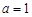 时,求函数
时,求函数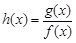 的单调减区间;
的单调减区间;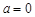 时,若
时,若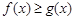 对任意的
对任意的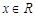 恒成立,求
恒成立,求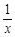 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 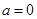 时,求
时,求 的极值;
的极值;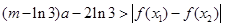 成立,求实数m的取值范围。
成立,求实数m的取值范围。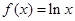 ,
,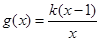 .
.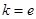 时,求函数
时,求函数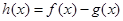 的单调区间和极值;
的单调区间和极值;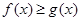 恒成立,求实数
恒成立,求实数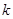 的值.
的值.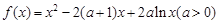 .
.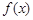 的单调区间;
的单调区间;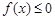 在区间
在区间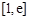 上恒成立,求实数
上恒成立,求实数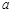 的取值范围.
的取值范围. 。
。 时,函数
时,函数 取得极值,求函数
取得极值,求函数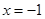 处的切线方程;
处的切线方程;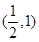 内不单调,求实数
内不单调,求实数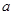 的取值范围。
的取值范围。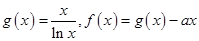 .
. 的单调区间;
的单调区间;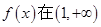 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;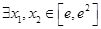 ,使
,使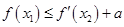 (
(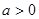 )成立,求实数a的取值范围.
)成立,求实数a的取值范围. 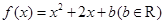 .
.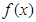 的值域为
的值域为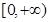 ,若关于
,若关于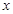 的不等式
的不等式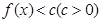 的解集为
的解集为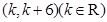 ,求
,求 的值;
的值;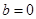 时,
时,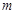 为常数,且
为常数,且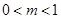 ,
,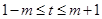 ,求
,求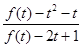 的取值范围.
的取值范围.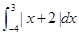 (2)
(2)