题目内容
已知函数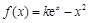 (其中
(其中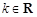 ,e是自然对数的底数).
,e是自然对数的底数).
(Ⅰ)若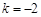 ,试判断函数
,试判断函数 在区间
在区间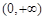 上的单调性;
上的单调性;
(Ⅱ)若函数 有两个极值点
有两个极值点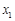 ,
,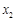 (
(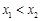 ),求k的取值范围;
),求k的取值范围;
(Ⅲ)在(Ⅱ)的条件下,试证明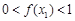 .
.
(Ⅰ) 在区间
在区间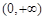 上是单调递减函数;(Ⅱ)k的取值范围是
上是单调递减函数;(Ⅱ)k的取值范围是 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
解析试题分析:(Ⅰ)将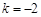 代入
代入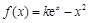 求导,根据其符号即可得其单调性;(Ⅱ)函数
求导,根据其符号即可得其单调性;(Ⅱ)函数 有两个极值点
有两个极值点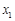 ,
,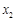 ,则
,则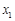 ,
,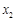 是
是 的两个根,即方程
的两个根,即方程 有两个根.接下来就研究函数
有两个根.接下来就研究函数 图象特征,结合图象便可知
图象特征,结合图象便可知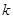 取何值时,方程
取何值时,方程 有两个根.
有两个根.
(Ⅲ)结合 图象可知,函数
图象可知,函数 的两个极值点
的两个极值点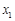 ,
,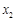 满足
满足 .
. ,这里面有
,这里面有 两个变量,那么能否换掉一个呢?
两个变量,那么能否换掉一个呢?
由 ,得
,得 ,利用这个关系式便可将
,利用这个关系式便可将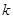 换掉而只留
换掉而只留 :
: ,这样根据
,这样根据 的范围,便可得
的范围,便可得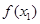 ,从而使问题得证.
,从而使问题得证.
试题解析:(Ⅰ)若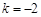 ,
,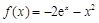 ,则
,则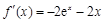 ,
,
当 时,
时, ,
,
故函数 在区间
在区间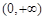 上是单调递减函数. 4分
上是单调递减函数. 4分
(Ⅱ)函数 有两个极值点
有两个极值点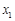 ,
,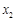 ,则
,则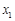 ,
,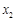 是
是 的两个根,
的两个根,
即方程 有两个根,设
有两个根,设 ,则
,则 ,
,
当 时,
时, ,函数
,函数 单调递增且
单调递增且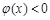 ;
;
当 时,
时, ,函数
,函数 单调递增且
单调递增且 ;
;
当 时,
时, ,函数
,函数 单调递减且
单调递减且 .
.
要使 有两个根,只需
有两个根,只需 ,
,
故实数k的取值范围是 . 9分
. 9分
(Ⅲ)由(Ⅱ)的解法可知,函数 的两个极值点
的两个极值点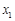 ,
,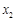 满足
满足 , 10分
, 10分
由 ,得
,得 ,
,
所以 ,
,
由于 ,故
,故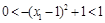 ,
,
所以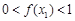 . 14分
. 14分
考点:1、导数的应用;2、不等关系.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
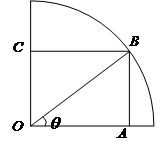
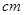 的圆形(
的圆形(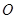 为圆心)铁皮上截取一块矩形材料
为圆心)铁皮上截取一块矩形材料 ,其中点
,其中点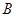 在圆弧上,点
在圆弧上,点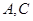 在两半径上,现将此矩形材料卷成一个以
在两半径上,现将此矩形材料卷成一个以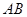 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设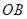 与矩形材料的边
与矩形材料的边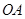 的夹角为
的夹角为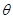 ,圆柱的体积为
,圆柱的体积为
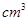 .
.
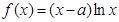 ,
,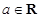 .
.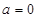 时,求函数
时,求函数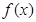 的极小值;
的极小值;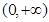 上为增函数,求
上为增函数,求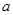 的取值范围.
的取值范围.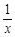 -(2+a)lnx(a≥0)
-(2+a)lnx(a≥0) 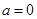 时,求
时,求 的极值;
的极值;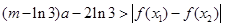 成立,求实数m的取值范围。
成立,求实数m的取值范围。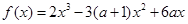
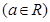 .
.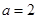 时,求函数
时,求函数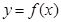 的单调区间;
的单调区间;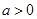 时,函数
时,函数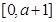 上的最大值为
上的最大值为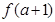 ,求
,求 的取值范围.
的取值范围.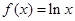 ,
,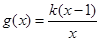 .
.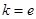 时,求函数
时,求函数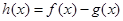 的单调区间和极值;
的单调区间和极值;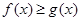 恒成立,求实数
恒成立,求实数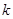 的值.
的值.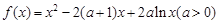 .
.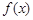 的单调区间;
的单调区间;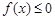 在区间
在区间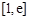 上恒成立,求实数
上恒成立,求实数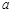 的取值范围.
的取值范围.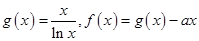 .
. 的单调区间;
的单调区间;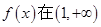 上是减函数,求实数a的最小值;
上是减函数,求实数a的最小值;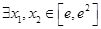 ,使
,使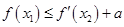 (
(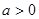 )成立,求实数a的取值范围.
)成立,求实数a的取值范围. 

 时,求
时,求 的单调区间;
的单调区间;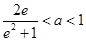 ,设
,设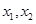 是函数
是函数 ,记
,记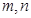 分别为
分别为 ,求实数
,求实数 的取值范围.
的取值范围.