题目内容
已知函数 .
.
(1)求函数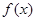 的最小正周期;
的最小正周期;
(2)求函数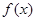 的递增区间;
的递增区间;
(3)当 时,求
时,求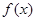 的值域.
的值域.
(1)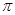 ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:解题思路:(1)利用二倍角公式的变形将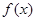 化成
化成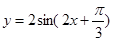 的形式,利用正弦函数的周期公式求周期;(2)解
的形式,利用正弦函数的周期公式求周期;(2)解 ;(3)由
;(3)由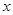 求
求 的范围,利用数形结合求值域.
的范围,利用数形结合求值域.
规律总结:凡是涉及三角函数的周期、定义域、值域、单调性、对称性等性质,一般思路是:利用三角恒等变换转化为 的形式.注意点:第(3)问中,一定要注意运用数形结合思想.
的形式.注意点:第(3)问中,一定要注意运用数形结合思想.
试题解析:



(1)  的最小正周期
的最小正周期
(2) 由
∴  的递增区间为
的递增区间为
(3) ∵  ∴
∴ 
∴ 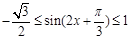 ∴
∴ 
∴  的值域为
的值域为 .
.
考点:1.三角恒等变换;2.三角函数的图像与性质;3.数形结合思想.

练习册系列答案
相关题目
某同学用“五点法”画函数 在某一
在某一
个周期内的图象时,列表并填入的部分数据如下表:
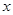 |  |  |  |  |  |
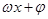 |  |  |  |  | 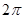 |
 |  |  |  |  |  |
(1)请求出上表中的
 ,并直接写出函数
,并直接写出函数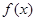 的解析式;
的解析式;(2)将
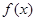 的图象沿
的图象沿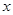 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数 ,若函数
,若函数 在
在 (其中
(其中 )上的值域为
)上的值域为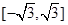 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求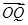 与
与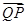 夹角
夹角 的大小.
的大小. 
 ;
; ,且
,且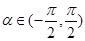 ,求
,求 的值.
的值.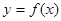 在区间
在区间 上的图像(完成列表并作图)。
上的图像(完成列表并作图)。

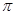

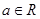 ,函数
,函数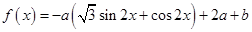 ,当
,当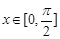 时,
时,  的值域是
的值域是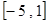 .
.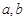 的值;
的值; 时,设
时,设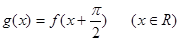 ,求
,求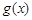 的单调区间.
的单调区间.
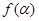 ;
;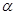 是第三象限角,且cos(
是第三象限角,且cos( )=
)= ,求
,求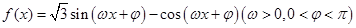 的图像过点
的图像过点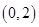 ,且函数
,且函数 图像的两相邻对称轴间的距离为
图像的两相邻对称轴间的距离为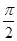 .
.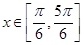 时,求函数
时,求函数 的值域;
的值域;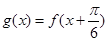 ,求函数
,求函数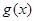 的单调区间.
的单调区间. .
.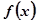 的最小正周期;
的最小正周期;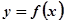 的图像向右、向上分别平移
的图像向右、向上分别平移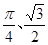 个单位长度得到
个单位长度得到 的图像,求
的图像,求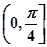 的最大值.
的最大值. ).
). 的最小正周期;
的最小正周期; ,求
,求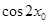 的值.
的值.
 的最小正周期;
的最小正周期;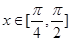 时,求
时,求