题目内容
已知 ,函数
,函数 ,当
,当 时,
时,  的值域是
的值域是 .
.
(1)求常数 的值;
的值;
(2)当 时,设
时,设 ,求
,求 的单调区间.
的单调区间.
(1) (2)
(2)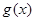 的单调递增区间为
的单调递增区间为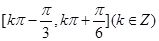 ,单调递减区间为
,单调递减区间为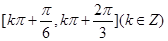
解析试题分析:(1)先由辅助角公式化为一个角的三角函数,按照复合函数求值域的方法,结合所给 的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域,注意分类讨论.(2)先利用诱导公式求出
的范围,求出内函数的值域,作为中间函数的定义域,利用三角函数图像求出中间函数的值域,作为外函数的定义域,再利用外函数的性质求出外函数的值域即为所求函数的值域,注意分类讨论.(2)先利用诱导公式求出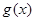 的解析式,利用复合函数单调区间的求法求出
的解析式,利用复合函数单调区间的求法求出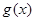 的单调区间.
的单调区间.
试题解析:(1)由题设知: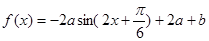 1分
1分
由 知:
知: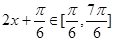 ,得
,得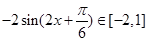 3分
3分
∴当 时,
时, 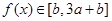 , 即
, 即 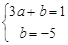 ,
, 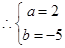 ; 5分
; 5分
当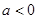 时,
时, 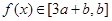 , 即
, 即 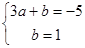
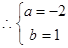 7分
7分
所以 8分
8分
(2)由(1)及题设知: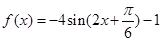 9分
9分
∴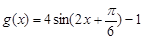 10分
10分
由 得
得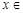
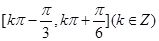
由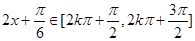 得
得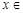
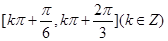 12分
12分
∴ 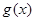 的单调递增区间为
的单调递增区间为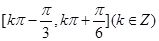
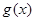 的单调递减区间为
的单调递减区间为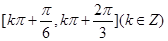 14分
14分
(其他写法参照给分)
考点:三角变换;三角函数在某个区间上的值域;诱导公式;三角函数单调性

练习册系列答案
相关题目

 ,
,

 的周期和单调递增区间;
的周期和单调递增区间; 在
在 上有解,求实数m的取值范围.
上有解,求实数m的取值范围. .
. 的解析式
的解析式 Acos(
Acos( )+B的形式,并用五点法作出
)+B的形式,并用五点法作出 的图像经过怎样的变换
的图像经过怎样的变换 的图像.
的图像. 和
和 为方程
为方程 的两根,求
的两根,求 ;(2)
;(2) 的值。
的值。 ;求
;求 的值.
的值. .
. 的最小正周期;
的最小正周期; 时,求
时,求
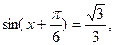 则
则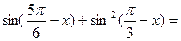 ____________
____________