题目内容
函数y=log2[(x-1)(3-x)]的定义域为( )
| A.(1,3) | B.[1,3] | C.(-∞,1)∪(3,+∞) | D.{x|x≠1且x≠3} |
由(x-1)(3-x)>0,
得(x-1)(x-3)<0,即1<x<3.
∴函数y=log2[(x-1)(3-x)]的定义域为(1,3).
故选:A.
得(x-1)(x-3)<0,即1<x<3.
∴函数y=log2[(x-1)(3-x)]的定义域为(1,3).
故选:A.

练习册系列答案
相关题目
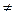 1,函数f (x) =alg(x2-2n+1)有最大值.则不等式logn(x2-5x+7)>0的解集为__ _.
1,函数f (x) =alg(x2-2n+1)有最大值.则不等式logn(x2-5x+7)>0的解集为__ _. ,那么
,那么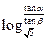 的值是( )
的值是( )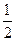
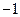
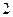
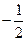
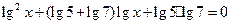 的两根是
的两根是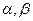 ,则
,则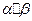 的值是____________
的值是____________ 的定义域为
的定义域为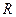 ,则
,则 的范围为__________。
的范围为__________。