题目内容
已知函数f(n)=logn+2(n+3)(n∈N*),使f(1)•f(2)…f(k)为整数的数k(k∈N*)且满足k在区间[1,100]内,则k的个数为( )
| A.1 | B.2 | C.3 | D.4 |
由题意可得f(1)•f(2)…f(k)=log34•log45•log56…log(k+2)(k+3)=log3(k+3)为整数,
可得 k+3=3n(n∈Z).
又∵k∈[1,100],k∈(N*),∴k=6,24,78,共计3个,
故选C.
可得 k+3=3n(n∈Z).
又∵k∈[1,100],k∈(N*),∴k=6,24,78,共计3个,
故选C.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
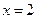 及
及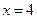 与函数
与函数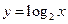 图像的交点分别为
图像的交点分别为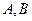 ,与函数
,与函数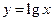 图像的交点分别为
图像的交点分别为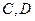 ,则直线AB与CD ( )
,则直线AB与CD ( )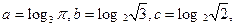 则( )
则( )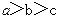
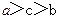
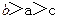
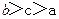
 且
且 ,求函数
,求函数 的最大值和最小值.
的最大值和最小值.