题目内容
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为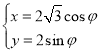 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 为曲线
为曲线![]() 上的一个动点,求点
上的一个动点,求点![]() 到直线
到直线![]() 距离的最小值.
距离的最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)直接把曲线![]() 的参数方程利用平方关系消去参数即可得到曲线的普通方程,把直线
的参数方程利用平方关系消去参数即可得到曲线的普通方程,把直线![]() 的极坐标方程展开两角和的余弦,结合
的极坐标方程展开两角和的余弦,结合![]() 可得直角坐标方程;
可得直角坐标方程;
(2)设![]() ,利用点到直线距离公式写出
,利用点到直线距离公式写出![]() 到直线
到直线![]() 的距离,结合三角函数求最值得答案.
的距离,结合三角函数求最值得答案.
(1)由曲线![]() 的参数方程得
的参数方程得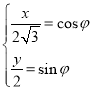 (
(![]() 为参数),
为参数),
消去参数![]() 得曲线
得曲线![]() 的普通方程为
的普通方程为![]() ;
;
由![]() ,得
,得![]() ,
,
化为直角坐标方程为![]() :
:![]() ;
;
(2)依题意,设![]() ,则
,则![]() 到直线
到直线![]() 的距离
的距离
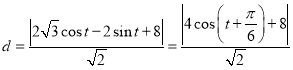
![]() ,
,
当![]() ,
,![]() ,即
,即![]() ,
,![]() 时,
时,![]() .
.
故点![]() 到直线
到直线![]() 距离的最小值为
距离的最小值为![]() .
.

【题目】为了保障某治疗新冠肺炎药品的主要药理成分在国家药品监督管理局规定的值范围内,武汉某制药厂在该药品的生产过程中,检验员在一天中按照规定从该药品生产线上随机抽取20件产品进行检测,测量其主要药理成分含量(单位:mg).根据生产经验,可以认为这条药品生产线正常状态下生产的产品的主要药理成分含量服从正态分布N(μ,σ2).在一天内抽取的20件产品中,如果有一件出现了主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对本次的生产过程进行检查.
(1)下面是检验员在2月24日抽取的20件药品的主要药理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
经计算得![]() xi=9.96,s
xi=9.96,s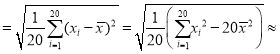 0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数
0.19;其中xi为抽取的第i件药品的主要药理成分含量,i=1,2,…,20.用样本平均数![]() 作为μ的估计值
作为μ的估计值![]() ,用样本标准差s作为σ的估计值
,用样本标准差s作为σ的估计值![]() ,利用估计值判断是否需对本次的生产过程进行检查?
,利用估计值判断是否需对本次的生产过程进行检查?
(2)假设生产状态正常,记X表示某天抽取的20件产品中其主要药理成分含量在(μ﹣3σ,μ+3σ)之外的药品件数,求/span>P(X=1)及X的数学期望.
附:若随机变量Z服从正态分布N(μ,σ2),则P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.