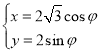题目内容
【题目】已知![]() .
.
(1)求![]() 的单调区间;
的单调区间;
(2)若![]() ,恒有
,恒有![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() 在
在![]() 和
和![]() 上单调递减(2)
上单调递减(2)![]()
【解析】
(1)求导后可得 ,令
,令![]() ,求导后可得
,求导后可得![]() 的单调性,进而可得
的单调性,进而可得![]() ,即可得解;
,即可得解;
(2)设![]() ,求导后可得
,求导后可得![]() ,令
,令![]() ,对
,对![]() 求导后可得
求导后可得![]() ,按照
,按照![]() 、
、![]() 分类讨论即可得解.
分类讨论即可得解.
(1)![]() 的定义域为
的定义域为![]() ,
, ,
,
令![]() ,则
,则![]() ,
,
注意到![]() 的定义域为
的定义域为![]() ,
,
因此![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
即![]() ,即
,即![]() 恒成立,
恒成立,
从而![]() 在
在![]() 和
和![]() 上单调递减.
上单调递减.
(2)不等式等价于![]() ,设
,设![]() ,
,
则![]() ,
,
设![]() ,则
,则![]() ,
,
注意到![]() 单调递增,且
单调递增,且![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 单调递增,
单调递增,
从而![]() ,
,
取![]() ,
,
则![]() ,
,
故![]() ,使得
,使得![]() ,从而
,从而![]() 在
在![]() 上单调递减,
上单调递减,
故当![]() 时,
时,![]() ,与题设矛盾;
,与题设矛盾;
令![]() ,则
,则![]() ,
,
则![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,
,
所以![]() 在
在![]() 上成立,
上成立,
当![]() 时,由
时,由![]() 可知:
可知:![]()
![]() ,
,
注意到![]() ,则
,则![]() 恒成立,
恒成立,
因此![]() 单调递增,从而
单调递增,从而![]() ,恒有
,恒有![]() ,符合题意.
,符合题意.
综上可知,![]() 的取值范围为
的取值范围为![]() .
.

【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 | 90.10% | 4.98% | 3.82% | 1.10% |
净利润占比 | 95.80% |
| 3.82% | 0.86% |
则下列判断中不正确的是( )
A.该公司2018年度冰箱类电器销售亏损
B.该公司2018年度小家电类电器营业收入和净利润相同
C.该公司2018年度净利润主要由空调类电器销售提供
D.剔除冰箱类销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
【题目】中国历法推测遵循以测为辅、以算为主的原则.例如《周髀算经》和《易经》里对二十四节气的晷(guǐ)影长的记录中,冬至和夏至的晷影长是实测得到的,其它节气的晷影长则是按照等差数列的规律计算得出的.下表为《周髀算经》对二十四节气晷影长的记录,其中![]() 寸表示115寸
寸表示115寸![]() 分(1寸=10分).
分(1寸=10分).
节气 | 冬至 | 小寒 (大雪) | 大寒 (小雪) | 立春 (立冬) | 雨水 (霜降) | 惊蛰 (寒露) | 春分 (秋分) | 清明 (白露) | 谷雨 (处暑) | 立夏 (立秋) | 小满 (大暑) | 芒种 (小暑) | 夏至 |
晷影长 (寸 | 135 |
|
|
|
|
| 75.5 |
|
|
|
|
| 16.0 |
已知《易经》中记录某年的冬至晷影长为130.0寸,夏至晷影长为14.8寸,按照上述规律那么《易经》中所记录的春分的晷影长应为( )
A.91.6寸B.82.0寸C.81.4寸D.72.4寸