题目内容
【题目】某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),
第5组[95,100]得到的频率分布直方图如图所示.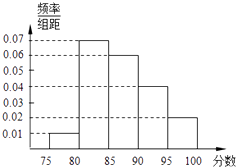
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,求第3,4,5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有一名学生被甲考官面试的概率.
【答案】
(1)解:根据所给的频率分步直方图中小正方形的长和宽,
得到第三组的频率为0.06×5=0.3;
第四组的频率为0.04×5=0.2;
第五组的频率为0.02×5=0.1.
(2)解:由题意知本题是一个等可能事件的概率,
由(1)可知第三,四,五组的频率分别为:0.3,0.2,0.1
则分层抽样第3,抽取的人数为: ![]() ×6=3
×6=3
第4组抽取的人数为: ![]() ×6=2
×6=2
5组每组抽取的人数为: ![]() ×6=1;
×6=1;
(3)解:学校决定在这6名学生中随机抽取2名学生接受甲考官的面试,
由题意知变量ξ的可能取值是0,1,2
该变量符合超几何分布,
∴P(ξ=i)= ![]() (i=0,1,2)
(i=0,1,2)
∴ξ分布列是

∴P(ξ≥1)= ![]() +
+ ![]() =
= ![]() =
= ![]()
【解析】(1)根据频率分步直方图的性质,根据所给的频率分步直方图中小矩形的长和宽,求出矩形的面积,即这组数据的频率.(2)由上一问求得频率,可知3,4,5组各自所占的比例样,根据分层抽样的定义进行求解;(3)由题意知变量ξ的可能取值是0,1,2,该变量符合超几何分布,根据超几何分布的概率公式写出变量的概率,写出这组数据的分布列从而求出P(ξ≥1)的概率;