题目内容
如图所示，AB与CD是⊙O的直径，AB⊥CD，P是AB延长线上一点，连PC交⊙O于点E，连DE交AB于点F，若AB=2BP=4，则PF=______．
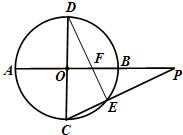
由题意得：CD是⊙O的直径，
且AB⊥CD，
∴Rt△DOF∽RtPEF，
∴
=
，
∴OF×PF=EF×DF．
又相交弦定理得：DF•FE=BF•AF，所以BF×AF=OF×PF；
设OF=x，BF=2-x，AF=2+x，PF=4-x
代入可求得x=1，
即PF=3．
故填：3．
且AB⊥CD，
∴Rt△DOF∽RtPEF，
∴
| OF |
| EF |
| DF |
| PF |
∴OF×PF=EF×DF．
又相交弦定理得：DF•FE=BF•AF，所以BF×AF=OF×PF；
设OF=x，BF=2-x，AF=2+x，PF=4-x
代入可求得x=1，
即PF=3．
故填：3．
练习册系列答案
相关题目
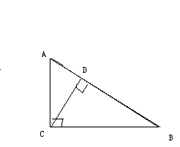
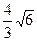，AC边上的中线BD＝
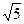，cosB＝
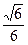，如图所示，
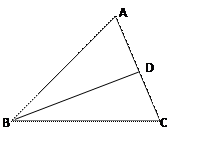求：sinA。
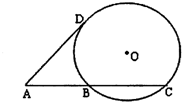
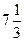，PO=12.求⊙O的半径。