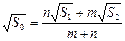题目内容
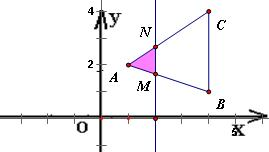
△ABC的顶点坐标分别为A(1,2),B(4,1),C(4,4),直线l平行于BC,截△ABC得到一个小三角形,且截得小三角形面积是△ABC面积的
,则直线l的方程为______.
| 1 |
| 9 |
∵B(4,1),C(4,4),
∴直线BC的方程为:x=4
又∵直线l平行于BC,
∴可设直线l方程为x=k(1<k<4)
设直线l分别与AB、AC交于点M、N,
由△AMN∽△ABC,且△AMN面积是△ABC面积的
,
得(
)2=
⇒MN=
BC=1
∵A(1,2),B(4,1)
∴直线AB的斜率为k1=
=-
可得直线AB方程为:y-2=-
(x-1),即y=-
x+
令x=k,得y=-
k+
,
∴M(k,-
k+
)
同理求得N(k,
k+
)
∴MN=
k+
-(-
k+
)=1⇒k=2
∴直线l的方程为x=2
故答案为:x=2
∴直线BC的方程为:x=4
又∵直线l平行于BC,
∴可设直线l方程为x=k(1<k<4)
设直线l分别与AB、AC交于点M、N,
由△AMN∽△ABC,且△AMN面积是△ABC面积的
| 1 |
| 9 |
得(
| MN |
| BC |
| 1 |
| 9 |
| 1 |
| 3 |
∵A(1,2),B(4,1)
∴直线AB的斜率为k1=
| 1-2 |
| 4-1 |
| 1 |
| 3 |
可得直线AB方程为:y-2=-
| 1 |
| 3 |
| 1 |
| 3 |
| 7 |
| 3 |
令x=k,得y=-
| 1 |
| 3 |
| 7 |
| 3 |
∴M(k,-
| 1 |
| 3 |
| 7 |
| 3 |
同理求得N(k,
| 2 |
| 3 |
| 4 |
| 3 |
∴MN=
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 7 |
| 3 |
∴直线l的方程为x=2
故答案为:x=2


练习册系列答案
相关题目
 线段
线段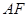 中,
中,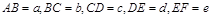 .则以A,B,C,D,E,F为端点的所有线段长度的和为:
.则以A,B,C,D,E,F为端点的所有线段长度的和为: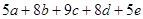
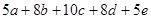
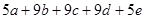
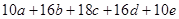
 的面积是1cm2,则
的面积是1cm2,则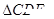 的面积是 cm2.
的面积是 cm2.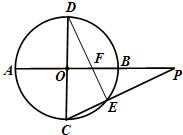



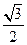 BD,
BD, 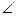 ABD=
ABD=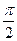 ,设
,设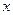 ,四边形ABCD的面积为S,求函数S=
,四边形ABCD的面积为S,求函数S=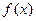 的最大值.
的最大值.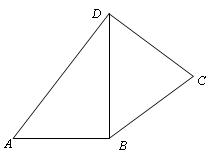
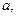
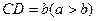 。若
。若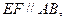 EF到CD与AB的距离之比为
EF到CD与AB的距离之比为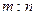 ,则可推算出:
,则可推算出: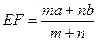 ,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设
,用类比的方法,推想出下列问题的结果,在上面的梯形ABCD中,延长梯形的两腰AD和BC交于O点,设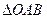 ,
,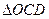 的面积分别为
的面积分别为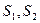 ,EF//AB,且EF到CD与AB的距离之比为
,EF//AB,且EF到CD与AB的距离之比为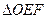 的面积
的面积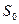 与
与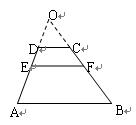
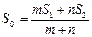 B
B 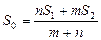
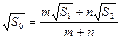 D
D