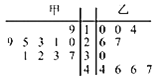
题目内容
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,PA=PD=CD=BC=1.
,PA=PD=CD=BC=1.
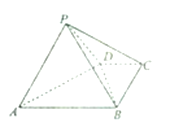
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见证明;(2)![]()
【解析】
(1)推导出AD⊥BD,PA⊥BD,从而BD⊥平面PAD,由此能证明平面PAD⊥平面ABCD.
(2)取AD中点O,连结PO,则PO⊥AD,以O为坐标原点,以过点O且平行于BC的直线为x轴,过点O且平行于AB的直线为y轴,直线PO为z轴,建立空间直角坐标系,利用空间向量法能求出直线PA与平面PBC所成角的正弦值.
(1)∵AB∥CD,∠BCD![]() ,PA=PD=CD=BC=1,
,PA=PD=CD=BC=1,
∴BD![]() ,∠ABC
,∠ABC![]() ,
,![]() ,∴
,∴![]() ,
,
∵AB=2,∴AD![]() ,∴AB2=AD2+BD2,∴AD⊥BD,
,∴AB2=AD2+BD2,∴AD⊥BD,
∵PA⊥BD,PA∩AD=A,∴BD⊥平面PAD,
∵BD平面ABCD,∴平面PAD⊥平面ABCD.
(2)取AD中点O,连结PO,则PO⊥AD,且PO![]() ,
,
由平面PAD⊥平面ABCD,知PO⊥平面ABCD,
以O为坐标原点,以过点O且平行于BC的直线为x轴,过点O且平行于AB的直线为y轴,
直线PO为z轴,建立如图所示的空间直角坐标系,
则A(![]() ,0),B(
,0),B(![]() ,0),C(
,0),C(![]() ,0),P(0,0,
,0),P(0,0,![]() ),
),
![]() (﹣1,0,0),
(﹣1,0,0),![]() (
(![]() ,
,![]() ),
),
设平面PBC的法向量![]() (x,y,z),
(x,y,z),
则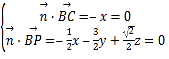 ,取z
,取z![]() ,得
,得![]() (0,
(0,![]() ,
,![]() ),
),
∵![]() (
(![]() ,
,![]() ),
),
∴cos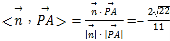 ,
,
∴直线PA与平面PBC所成角的正弦值为![]() .
.

 阅读快车系列答案
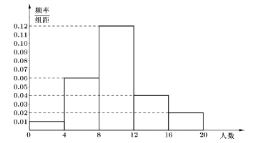
阅读快车系列答案【题目】某经销商从沿海城市水产养殖厂购进一批某海鱼,随机抽取50条作为样本进行统计,按海鱼重量(克)得到如图的频率分布直方图:
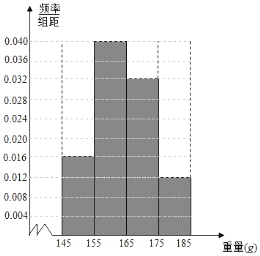
(1)若经销商购进这批海鱼100千克,试估计这批海鱼有多少条(同一组中的数据用该区间的中点值作代表);
(2)根据市场行情,该海鱼按重量可分为三个等级,如下表:
等级 | 一等品 | 二等品 | 三等品 |
重量(g) |
|
|
|
若经销商以这50条海鱼的样本数据来估计这批海鱼的总体数据,视频率为概率.现从这批海鱼中随机抽取3条,记抽到二等品的条数为X,求x的分布列和数学期望.