题目内容
12．若变量x，y满足约束条件$\left\{\begin{array}{l}{2x+3y≥6}\\{x-y≥0}\\{x≤3}\end{array}\right.$，则函数z=2x+y的最大值和最小值分别是（ ）| A． | 9和6 | B． | 6和$\frac{18}{5}$ | C． | 9和5 | D． | 9和$\frac{18}{5}$ |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，即可求最大值和最小值．
解答 解：作出不等式组对应的平面区域如图：（阴影部分）．
由z=2x+y得y=-2x+z，
平移直线y=-2x+z，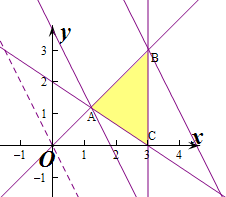
由图象可知当直线y=-2x+z经过点C时，直线y=-2x+z的截距最大，
此时z最大．
由$\left\{\begin{array}{l}{x=3}\\{x-y=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$，即B（3，3），
代入目标函数z=2x+y得z=2×3+3=9．
即目标函数z=2x+y的最大值为9．
当直线y=-2x+z经过点A时，直线y=-2x+z的截距最小，
此时z最小．
由$\left\{\begin{array}{l}{2x+3y=6}\\{x-y=0}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=\frac{6}{5}}\\{y=\frac{6}{5}}\end{array}\right.$，即A（$\frac{6}{5}$，$\frac{6}{5}$），
代入目标函数z=2x+y得z=2×$\frac{6}{5}$+$\frac{6}{5}$=$\frac{18}{5}$．
即目标函数z=2x+y的最小值为$\frac{18}{5}$．
则z=2x+y的最大值和最小值分别是9和$\frac{18}{5}$，
故选：D
点评 本题主要考查线性规划的应用，利用目标函数的几何意义，结合数形结合的数学思想是解决此类问题的基本方法．
练习册系列答案
天天练口算系列答案
相关题目
设b＞0，椭圆方程为$\frac{{x}^{2}}{2{b}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1，抛物线方程为y=$\frac{1}{8}$x2+b，如图所示，过点F（0，b+2）作x轴的平行线，与抛物线在第一象限的焦点为G，已知抛物线在G点的切线经过椭圆的右焦点F1
7．已知m、n是两条不同的直线，α、β是两个不同的平面，则下列命题正确的是（ ）
| A． | 若m∥n，m∥α且n∥β，则α∥β?????????? | |
| B． | 若m⊥n，m∥α且n∥β，则α⊥β? | |
| C． | 若m∥α且n⊥m，则n⊥α???????????????????? | |
| D． | 若m⊥n，m⊥α且n⊥β，则α⊥β |