题目内容
设a≠0,对于函数f(x)=log3(ax2-x+a),
(1)若x∈R,求实数a的取值范围;
(2)若f(x)∈R,求实数a的取值范围.
(1)若x∈R,求实数a的取值范围;
(2)若f(x)∈R,求实数a的取值范围.
(1)f(x)的定义域为R,则ax2-x+a>0对一切实数x恒成立,其等价条件是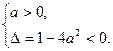 解得a>
解得a>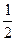 .
.
(2)f(x)的值域为R,则真数ax2-x+a能取遍大于0的所有实数,其等价条件是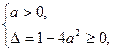 解得0<a≤
解得0<a≤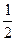 .
.
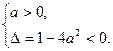 解得a>
解得a>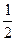 .
.(2)f(x)的值域为R,则真数ax2-x+a能取遍大于0的所有实数,其等价条件是
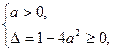 解得0<a≤
解得0<a≤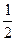 .
. f(x)的定义域是R,等价于ax2-x+a>0对一切实数都成立,而f(x)的值域为R,等价于其真数ax2-x+a能取遍大于0的所有实数值,(1)与(2)虽只有一字之差,但结果却大不相同.

练习册系列答案
相关题目
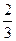 <1,则a的取值范围是____________.
<1,则a的取值范围是____________.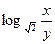 的值.
的值.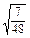 +log212-
+log212-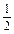 log242-1;
log242-1;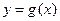 的图象如下图所示,则函数
的图象如下图所示,则函数 的图象大致是
的图象大致是
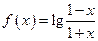 ,
,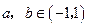 求证:
求证: .
.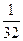
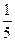 lg2
lg2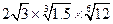 ;(2)
;(2)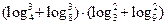 .
.