题目内容
(本小题满分14分)
已知函数f(x)=(x2+ax-2a-3)·e3-x (a∈R)
(1)讨论f(x)的单调性;
(2)设g(x)=(a2+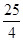 )ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
)ex(a>0),若存在x1,x2∈[0,4]使得|f(x1)-g(x2)|<1成立,求a的取值范围.
【答案】
⑴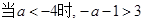 ,此时
,此时 在
在 上为减函数,在
上为减函数,在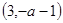 上为增函数,在
上为增函数,在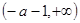 上为减函数;
上为减函数;
当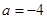 时,
时,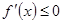 ,此时
,此时 在
在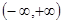 上为减函数;
上为减函数;
当 时,此时
时,此时 在
在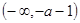 上为减函数,在
上为减函数,在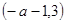 上为增函数,在
上为增函数,在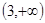 上为减函数.
上为减函数.
⑵ a的取值范围为 .
.
【解析】
试题分析:⑴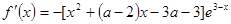 ,令
,令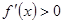 ,
,
即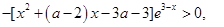 所以
所以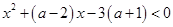
所以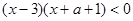 …………………………………………………………………3分
…………………………………………………………………3分
 ,此时
,此时 在
在 上为减函数,在
上为减函数,在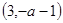 上为增函数,在
上为增函数,在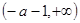 上为减函数;
上为减函数;
当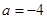 时,
时,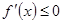 ,此时
,此时 在
在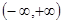 上为减函数;
上为减函数;
当 时,此时
时,此时 在
在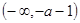 上为减函数,在
上为减函数,在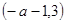 上为增函数,在
上为增函数,在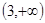 上为减函数.
………………………………………………………………………………6分
上为减函数.
………………………………………………………………………………6分
⑵ 当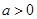 时,
时,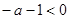 ,则
,则 在
在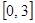 上为增函数,在
上为增函数,在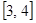 上为减函数
上为减函数
又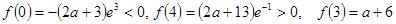
∴ 在
在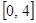 上的值域为
上的值域为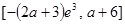 ………………………………………8分
………………………………………8分
又 在
在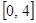 上为增函数,其值域为
上为增函数,其值域为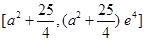 ……10分
……10分
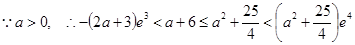
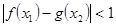 等价于
等价于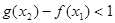 ……………………………………………12分
……………………………………………12分
 存在
存在 使得
使得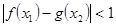 成立,只须
成立,只须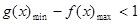
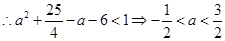 ,又
,又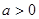
∴a的取值范围为 .
………………………………………………………………14分
.
………………………………………………………………14分
考点:本题主要考查应用导数研究函数的单调性,恒成立问题。
点评:典型题,本题属于导数应用中的基本问题,(2)涉及恒成立问题,转化成求函数的最值,这种思路是一般解法,往往要利用“分离参数法”,本题最终化为最值之间故选的研究,体现考题“起点高,落点低”的特点。

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)