��Ŀ����
 ��֪��Բ������������ԭ�㣬������x���ϣ����ҽ���Ϊ2�������볤��ı���
��֪��Բ������������ԭ�㣬������x���ϣ����ҽ���Ϊ2�������볤��ı���
| ||
| 2 |
��1������Բ�ķ��̣�
��2����֪��Բ�������¶���������Բ
| x2 |
| a2 |
| y2 |
| b2 |
| x0x |
| a2 |
| y0y |
| b2 |
| 3 |
| 2 |
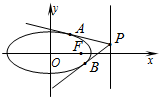
��3����ͼ������Բ��������һ��P������Բ����������PA��PB���е�ΪA��B����֤��A��F��B���㹲�ߣ�
��������1������Բ�ķ���Ϊ
+
=1������c=1��
=
��a2=b2+c2����ü��ɣ�
��2�����ø����Ķ������뼴�ɣ�
��3������Բ�����ϵĵ�P��4��y0����A��x1��y1����B��x2��y2�������ã�2���и����Ķ����ɵã�����PA��PB�������õ�ֱ��AB�ķ�����x+
y=1����F��1��0������˷��̣�����֤��A��F��B���ߣ�
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| ||
| 2 |
��2�����ø����Ķ������뼴�ɣ�
��3������Բ�����ϵĵ�P��4��y0����A��x1��y1����B��x2��y2�������ã�2���и����Ķ����ɵã�����PA��PB�������õ�ֱ��AB�ķ�����x+
| y0 |
| 3 |
���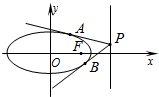 �⣺��1������Բ�ķ���Ϊ
�⣺��1������Բ�ķ���Ϊ
+
=1����c=1��
=
����a2=b2+c2��
�������a=2��b=
��
����Բ�ķ���Ϊ
+
=1��
��2���ɶ����ù���A(1��
)�����ߵķ���Ϊ
+
=1����x+2y-4=0��
��3������Բ�����ϵĵ�P��4��y0����A��x1��y1����B��x2��y2����
��AP�ķ���Ϊ
+
=1��BP�ķ���Ϊ
+
=1��
�ֵ�P��4��y0�������������ϣ���x1+
y1=1��x2+
y2=1��
��ֱ��AB�ķ�����x+
y=1��
��ֱ�߹���F��1��0������A��F��B���ߣ�
 �⣺��1������Բ�ķ���Ϊ
�⣺��1������Բ�ķ���Ϊ| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
| ||
| 2 |
�������a=2��b=
| 3 |
����Բ�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2���ɶ����ù���A(1��
| 3 |
| 2 |
| x |
| 4 |
| y |
| 2 |
��3������Բ�����ϵĵ�P��4��y0����A��x1��y1����B��x2��y2����
��AP�ķ���Ϊ
| x1x |
| 4 |
| y1y |
| 3 |
| x2x |
| 4 |
| y2y |
| 3 |
�ֵ�P��4��y0�������������ϣ���x1+
| y0 |
| 3 |
| y0 |
| 3 |
��ֱ��AB�ķ�����x+
| y0 |
| 3 |
��ֱ�߹���F��1��0������A��F��B���ߣ�
���������⿼������Բ�ı����̼������ʡ����ߵ����ʡ����㹲�ߵȻ���֪ʶ��������ܷ������������⣮

��ϰ��ϵ�д�
�����Ŀ
 ��֪��Բ������������ԭ��O��������x���ϣ����᳤Ϊ2������������Ͷ���������˵�ǡΪһ�������εĶ��㣮���ҽ���F��x���ֱ��ֱ��l����Բ��P��Q���㣮
��֪��Բ������������ԭ��O��������x���ϣ����᳤Ϊ2������������Ͷ���������˵�ǡΪһ�������εĶ��㣮���ҽ���F��x���ֱ��ֱ��l����Բ��P��Q���㣮