题目内容
已知直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.
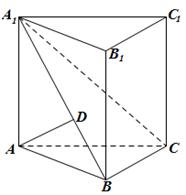
(1)求证:平面A1BC⊥平面ABB1A1;
(2)若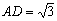 ,AB=BC=2,P为AC中点,求三棱锥
,AB=BC=2,P为AC中点,求三棱锥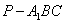 的体积。
的体积。
【答案】
(1)利用线线垂直证明线面垂直;(2) 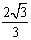
【解析】
试题分析:直三棱柱ABC-A1B1C1中,A A1⊥平面ABC,
∴A A1⊥BC,
∵AD⊥平面A1BC,
∴AD⊥BC,
∵A A1,AD为平面ABB1A1内两相交直线,
∴BC⊥平面ABB1A1,
又∵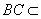 平面A1BC,
平面A1BC,
∴平面A1BC⊥平面ABB1A1 7分
(2) 由等积变换得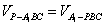 ,
,
在直角三角形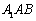 中,由射影定理(
中,由射影定理(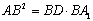 )知
)知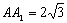 ,
,
∵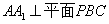 ,
,
∴三棱锥的高为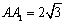 10分
10分
又∵底面积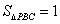 12分
12分
∴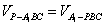 =
=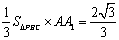 14分
14分
法二:连接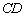 ,取
,取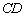 中点
中点 ,连接
,连接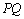 ,∵P为AC中点,
,∵P为AC中点,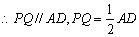
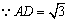 ,
,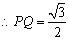 ,
9分
,
9分
由(1)AD⊥平面A1BC,∴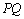 ⊥平面A1BC,
⊥平面A1BC,
∴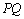 为三棱锥P- A1BC的高,
11分
为三棱锥P- A1BC的高,
11分
由(1)BC⊥平面ABB1A1 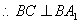 ,
,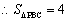 12分
12分
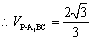 ,
14分
,
14分
考点:本题考查了空间中的线面关系
点评:高考中常考查空间中平行关系与垂直关系的证明以及几何体体积的计算,这是高考的重点内容.证明的关键是熟练掌握并灵活运用相关的判定定理与性质定理

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.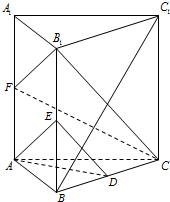 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.