Question

如图，已知直三棱柱ABC-A₁B₁C₁中，AB=AC；M．N．P分别是棱BC．CC₁．B₁C₁的中点．A1Q=3QA， BC=

2

AA1
（Ⅰ）求证：PQ∥平面ANB₁；
（Ⅱ）求证：平面AMN⊥平面AMB₁．

Answer 1

分析：（Ⅰ）取B₁N中点S连PS，证明PQ∥AS，通过PQ?平面ANB₁，AS?平面ANB₁，说明PQ∥平面ANB₁．
（Ⅱ）证明AM⊥BC，AM⊥MN，在直角△CMN和△BMB₁中，证明MN⊥MB₁，MN⊥平面AMB₁即可证明平面AMN⊥平面AMB₁．

解答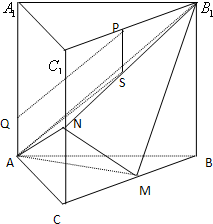：（本小题满分12分）
证明：（Ⅰ）取B₁N中点S连PS则PS∥CC₁，QA∥CC₁∴PS∥QA，
且PS=

1

4

CC₁=QA∴PSAQ为
平行四边形，…（3分）
∴PQ∥AS，又PQ?平面ANB₁，AS?平面ANB₁，
∴PQ∥平面ANB₁…（6分）
（Ⅱ）∵AB=AC，M是棱BC的中点，
∴AM⊥BC
又三棱柱为直三棱柱，∴CC₁⊥平面ABC，CC₁⊥AM
∴AM⊥平面CBB₁C₁，AM⊥MN…（9分）
在直角△CMN和△BMB₁中，

CM

NC

=

BC

BB1

=

2

，

BB1

BM

=

BB1

1 2 BC

=

2

   
 直角△CMN∽直角△BB₁M
∴MN⊥MB₁
又AM∩MB₁=M，∴MN⊥平面AMB₁；
∴平面AMN⊥平面AMB₁．…（12分）

点评：本题考查直线与平面平行的判定定理，平面与平面垂直的证明，考查空间想象能力，逻辑推理能力．