题目内容
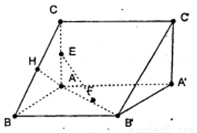
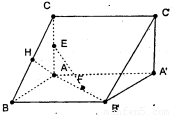
 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,(I)证明:EF⊥AH;
(II)求四面体E-FAH的体积.
分析:(I)连接B'C,得△AB'C中EF是中位线,所以B'C∥EF.由线面垂直的判定与性质,可证出AH⊥平面BB'C'C,从而得到AH⊥B'C,结合平行线的性质可得EF⊥AH;
(II)取AB的中点I,连接FI.可得△ABB'中,FI∥BB'且FI=
BB'=1.结合BB'⊥平面ABC,得FI⊥平面ABC,可得FI是三棱锥F-AEH的高线.求出△AEH的面积,结合锥体体积公式,可得三棱锥F-AEH的体积,即为四面体E-FAH的体积.
(II)取AB的中点I,连接FI.可得△ABB'中,FI∥BB'且FI=
| 1 |
| 2 |
解答:解:(I) 连接B'C,
连接B'C,
∵△AB'C中,E、F分别是AC、AB'的中点,∴B'C∥EF
∵BB'⊥平面ABC,AH⊆平面ABC,∴BB'⊥AH
∵△ABC中,AB=AC,H是BC的中点,∴BC⊥AH
又∵BB'、BC是平面BB'C'C内的相交直线
∴AH⊥平面BB'C'C
∵B'C⊆平面BB'C'C,∴AH⊥B'C
又∵B'C∥EF,∴AH⊥EF,即EF⊥AH;
(II) 取AB的中点I,连接FI
取AB的中点I,连接FI
∵△ABB'中,FI是中位线
∴FI∥BB'且FI=
BB'=1
∵BB'⊥平面ABC,
∴FI⊥平面ABC,可得FI是三棱锥F-AEH的高线
∵△ABC中,AB⊥AC且AB=AC=2
∴S△ABC=
×2×2=2,可得S△AEH=
S△ABC=
因此,三棱锥F-AEH的体积V=
S△AEH×EI=
×
×1=
∴四面体E-FAH的体积VE-FAH=VF-AEH=
 连接B'C,
连接B'C,∵△AB'C中,E、F分别是AC、AB'的中点,∴B'C∥EF
∵BB'⊥平面ABC,AH⊆平面ABC,∴BB'⊥AH
∵△ABC中,AB=AC,H是BC的中点,∴BC⊥AH
又∵BB'、BC是平面BB'C'C内的相交直线
∴AH⊥平面BB'C'C
∵B'C⊆平面BB'C'C,∴AH⊥B'C
又∵B'C∥EF,∴AH⊥EF,即EF⊥AH;
(II)
 取AB的中点I,连接FI
取AB的中点I,连接FI∵△ABB'中,FI是中位线
∴FI∥BB'且FI=
| 1 |
| 2 |
∵BB'⊥平面ABC,
∴FI⊥平面ABC,可得FI是三棱锥F-AEH的高线
∵△ABC中,AB⊥AC且AB=AC=2
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
因此,三棱锥F-AEH的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴四面体E-FAH的体积VE-FAH=VF-AEH=
| 1 |
| 6 |
点评:本题在特殊三棱柱中,证明线面平行并且求四面体的体积,着重考查了空间平行与垂直的证明和锥体体积公式等知识,属于中档题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目