题目内容
18.已知f(x)=x3+3ax2+bx+a2(a>1)在x=-1时有极值0.(1)求常数 a,b的值;
(2)方程f(x)=c在区间[-4,0]上有三个不同的实根时,求实数c的范围.
分析 (1)求出函数f(x)的导函数,由f(x)=x3+3ax2+bx+a2在x=-1时有极值O,则f(-1)=0,f′(-1)=0,两式联立可求常数a,b的值;
(2)把a,b代入后得到函数解析式,运用函数的导函数大于0和小于0求解函数f(x)的单调区间和函数f(x)的极值,再求出f(-4)和f(0),结合函数的单调性作出函数图象的大致形状,数形结合可求得实数c的范围.
解答 解:(1)由f(x)=x3+3ax2+bx+a2,得:f′(x)=3x2+6ax+b
因为f(x)=x3+3ax2+bx+a2在x=-1时有极值O,
所以$\left\{\begin{array}{l}{f′(-1)=0}\\{f(-1)=0}\end{array}\right.$,即$\left\{\begin{array}{l}{3-6a+b=0}\\{-1+3a-b+{a}^{2}=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}a=1\\ b=3\end{array}\right.$或$\left\{\begin{array}{l}a=2\\ b=9\end{array}\right.$,
当a=1,b=3时,f(x)=x3+3x2+3x+1,
f′(x)=3x2+6x+3=3(x2+2x+1)=3(x+1)2≥0
所以函数f(x)=x3+3x2+3x+1在(-∞,+∞)上为增函数,
不满足在x=-1时有极值O,应舍掉,
所以,常数a,b的值分别为a=2,b=9;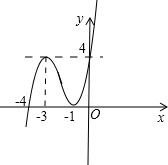
(2)当a=2,b=9时,f(x)=x3+6x2+9x+4,
f′(x)=3x2+12x+9,
由3x2+12x+9>0,得:x<-3或x>-1,
由3x2+12x+9<0,得:-3<x<-1.
所以,函数f(x)=x3+6x2+9x+4的增区间为(-∞,-3),(-1,+∞).减区间为(-3,-1).
又f(-4)=0,f(-3)=4,f(-1)=0,f(0)=4,
所以函数f(x)=x3+6x2+9x+4的大致图象如图,
若方程f(x)=C在区间[-4,0]上有三个不同的实根,则函数y=f(x)与y=C的图象有三个不同的交点,
由图象可知方程f(x)=C在区间[-4,0]上有三个不同的实根时实数c的范围是(0,4).
点评 本题考查了利用导数研究函数的单调性和极值,函数在某区间上的导函数大于0,函数在该区间上为增函数,函数在某区间上的导函数小于0,函数在该区间上为减函数,考查了数形结合的解题思想,同时训练了函数在极值点处的导数等于0,此题是中档题.


| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 内含 |
| A. | -16 | B. | -4 | C. | 4 | D. | -4或4 |