题目内容
【题目】某工厂生产一种产品，根据预测可知，该产品的产量平稳增长，记2015年为第1年，第x年与年产量
（万件）之间的关系如下表所示：
x | 1 | 2 | 3 | 4 |
| 4.00 | 5.52 | 7.00 | 8.49 |
现有三种函数模型：
，
，
（1）找出你认为最适合的函数模型，并说明理由，然后选取
这两年的数据求出相应的函数解析式；
（2）因受市场环境的影响，2020年的年产量估计要比预计减少30%，试根据所建立的函数模型，估计2020年的年产量.
【答案】（1）模型为
较好，理由见解析，相应的函数为
（2）8.05万件
【解析】
（1）根据单调性排除
，检验
，发现数据差距比较大，选择数据差距较小；
（2）根据（1）计算出的模型方程计算
即可得解.
解：（1）符合条件的函数模型是
若模型为，
由已知得
，∴
，
，
∴
所以
，
，与已知差距较大；
若模型为
，
为减函数，与已知不符；
若模型为，由，
∴
，
，
∴，所以
，
，与已知符合较好.
所以相应的函数为
（2）2020年预计年产量为
，所以2020年产量应为8.05万件
【题目】某大型高端制造公司为响应(中国制造2025)中提出的坚持“创新驱动、质量为先、绿色发展、结构优化、人才为本”的基本方针,准备加大产品研发投资,下表是该公司2017年5~12月份研发费用(百万元)和产品销量(万台)的具体数据:
月份 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
研发费用 | 2 | 3 | 6 | 10 | 21 | 13 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 2.5 | 6 | 3.5 | 3.5 | 4.5 |
（1）根据数据可知
与 
之间存在线性相关关系.
(i)求出关于的线性回归方程(系数精确到0.001);
(ii)若2018年6月份研发投人为25百万元，根据所求的线性回归方估计当月产品的销量;
(2)为庆祝该公司9月份成立30周年,特制定以下奖励制度:以
(单位:万台)表示日销量，
,则每位员工每日奖励200元;
,则每位员工每日奖励300元;
,则每位员工每日奖励400元.现已知该公司9月份日销量(万台)服从正态分布
,请你计算每位员工当月(按30天计算)获得奖励金额总数大约多少元
参考数据: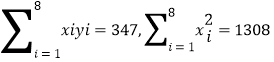
.
参考公式:对于一组数据
.其回归直线
的斜率和截距的最小二乘估计分别为
若随机变量
服从正态分布
,则
.
