题目内容
【题目】已知函数
，
.
（1）
恒成立的实数
的最大值
；
（2）设
，
，且满足
，求证：
.
【答案】（1）
；（2）见解析
【解析】
（1）化为分段函数，根据函数单调性即可求出函数的最小值，即可求出
的值，
（2）由m＞0，n＞0，且
，即：
，化简
≥2|m+2n|，由2|m+2n|＝2（m+2n）＝2（m+2n）
（
）
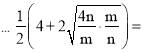4即可证得.
（1）已知函数
，
.由题意得，
恒成立，
即h（x）=
=2|x﹣1|﹣|x+1|＝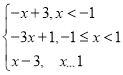
，
显然，h（x）在（﹣∞，1]上单调递减，在（1，+∞）上单调递增，
∴h（x）min＝h（1）＝﹣2，∴t
﹣2，即最大值=-2.
（2）由于m＞0，n＞0，且，即：，
=
+
=2（|m+1|+|2n﹣1|）≥2|m+2n|，
∴2|m+2n|＝2（m+2n）＝2（m+2n）（）
，
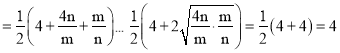当且仅当
，即当n＝
，m＝
时取“＝”，
故
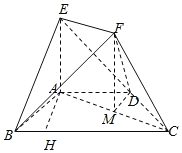
阅读快车系列答案【题目】某城市自2014年至2019年每年年初统计得到的人口数量如表所示.
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数（单位：万） | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
（1）设第
年的人口数量为
（2014年为第1年），根据表中的数据，描述该城市人口数量和2014年至2018年每年该城市人口的增长数量的变化趋势；
（2）研究统计人员用函数
拟合该城市的人口数量，其中
的单位是年.假设2014年初对应
，
的单位是万.设的反函数为
，求
的值（精确到0.1），并解释其实际意义.
【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜，售价8元/千克，若每天下午4点以前所购进的绿色蔬菜没有售完，则对未售出的绿色蔬菜降价处理，以3元/千克出售．根据经验，降价后能够把剩余蔬菜全部处理完毕，且当天不再进货．该生鲜批发店整理了过往30天（每天下午4点以前）这种绿色蔬菜的日销售量（单位：千克）得到如下统计数据（视频率为概率）（注：x，y∈N*）
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
（1）求在未来3天中，至少有1天下午4点前的销售量不少于450千克的概率．
（2）若该生鲜批发店以当天利润期望值为决策依据，当购进450千克比购进500千克的利润期望值大时，求x的取值范围．
