题目内容
6.在1和100间插入n个正数,使这n+2个正数成等比数列,则插入的n个正数之积为 ( )| A. | 10n | B. | n10 | C. | 100n | D. | n100 |
分析 由题意,在1和100之间插入n个正数,使得这n+2个数构成等比数列,由等比数列的性质易得n个正数之积Tn=$10{0}^{\frac{n}{2}}=1{0}^{n}$.
解答 解:由题意,在1和100之间插入n个正数,使得这n+2个数构成等比数列,将插入的n个正数之积记作Tn,
由等比数列的性质,序号的和相等,则项的乘积也相等知Tn=$10{0}^{\frac{n}{2}}=1{0}^{n}$,
故选:A.
点评 本题考查等比数列的性质,是基础的计算题.

练习册系列答案
相关题目
11.函数y=3x2+ax+4在区间[-1,1]上不是单调函数,则实数a的取值范围是( )
| A. | (-6,6) | B. | [-6,6] | C. | (-∞,-6]∪[6,+∞) | D. | (-∞,-6)∪(6,+∞) |
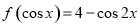 ,则
,则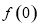 的值为( )
的值为( )