��Ŀ����
 �������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
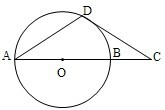
�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮A��AB��ԲO��ֱ����DΪԲO��һ�㣬��D��ԲO�����߽�AB�ӳ����ڵ�C����DA=DC����֤��AB=2BC��
B����ƽ��ֱ������ϵxOy�У���֪��A��0��0����B��-2��0����C��-2��1������kΪ����ʵ��������M=
|
|
C���ڼ�����ϵ�У���֪Բ��=2cos����ֱ��3��cos��+4��sin��+a=0���У���ʵ��a��ֵ��
D����a��b�ǷǸ�ʵ������֤��a3+b3��
| ab |
������A������OD����OD��DC����OA=OD��DA=DC�����ԡ�DAO=��ODA=��DCO����֤��OB=BC=OD=OA��������⣮
B���������MN=
=
�����ݾ�������㷨�������⣮
C���ڼ�����ϵ�У���֪Բ��=2cos����ֱ��3��cos��+4��sin��+a=0���У������⽫Բ��ֱ���Ȼ�Ϊһ�㷽�����꣬Ȼ���ټ���aֵ��
D�����ò���ʽ�����ʽ��з���֤����a3+b3-
(a2+b2)=a2
(
-
)+b2
(
-
)Ȼ���ٽ���������֤��
B���������MN=
|
|
|
C���ڼ�����ϵ�У���֪Բ��=2cos����ֱ��3��cos��+4��sin��+a=0���У������⽫Բ��ֱ���Ȼ�Ϊһ�㷽�����꣬Ȼ���ټ���aֵ��
D�����ò���ʽ�����ʽ��з���֤����a3+b3-
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
����⣺A��������һ��֤��������OD����OD��DC��
��OA=OD��DA=DC�����ԡ�DAO=��ODA=��DCO��
��DOC=��DAO+��ODA=2��DCO��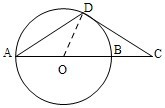
���ԡ�DCO=30�㣬��DOC=60�㣬
����OC=2OD����OB=BC=OD=OA������AB=2BC��
����������֤��������OD��BD��
��ΪAB��ԲO��ֱ�������ԡ�ADB=90�㣬AB=2OB��
��ΪDC��ԲO�����ߣ����ԡ�CDO=90�㣮
����ΪDA=DC�����ԡ�DAC=��DCA��
���ǡ�ADB�ա�CDO���Ӷ�AB=CO��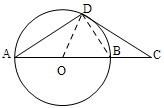
��2OB=OB+BC����OB=BC��
��AB=2BC��
B���֣�10�֣����������MN=
=
��
=
����֪A1��0��0����B1��0��-2����C1��k��-2����
����á�ABC����������1����A1B1C1�������|k|����������֪��|k|=2��1=2��
����k��ֵΪ2��-2��
C�⣺��2=2��cos�ȣ�Բ��=2cos�ȵ���ͨ����Ϊ��x2+y2=2x����x-1��2+y2=1��
ֱ��3��cos��+4��sin��+a=0����ͨ����Ϊ��3x+4y+a=0��
��Բ��ֱ�����У�����
=1��
��ã�a=2����a=-8��
D������һ��֤����a3+b3-
(a2+b2)=a2
(
-
)+b2
(
-
)
=(
-
)[(
)5-(
)5]
=(
-
)2[(
)4+(
)3(
)+(
)2(
)2+(
)(
)3+(
)4]
��Ϊʵ��a��b��0��(
-
)2��0��[(
)4+(
)3(
)+(
)2(
)2+(
)(
)3+(
)4]��0
������ʽ��0������a3+b3��
(a2+b2)��
����������֤������a��b�ǷǸ�ʵ���������a3+b3-
(a2+b2)
=a2
(
-
)+b2
(
-
)
=(
-
)[(
)5-(
)5]
��a��bʱ��
��
���Ӷ�(
)5��(
)5����(
-
)[(
)5-(
)5]��0��
��a��bʱ��
��
���Ӷ�(
)5��(
)5����(
-
)[(
)5-(
)5]��0��
����a3+b3��
(a2+b2)��
��OA=OD��DA=DC�����ԡ�DAO=��ODA=��DCO��
��DOC=��DAO+��ODA=2��DCO��

���ԡ�DCO=30�㣬��DOC=60�㣬
����OC=2OD����OB=BC=OD=OA������AB=2BC��
����������֤��������OD��BD��
��ΪAB��ԲO��ֱ�������ԡ�ADB=90�㣬AB=2OB��
��ΪDC��ԲO�����ߣ����ԡ�CDO=90�㣮
����ΪDA=DC�����ԡ�DAC=��DCA��
���ǡ�ADB�ա�CDO���Ӷ�AB=CO��

��2OB=OB+BC����OB=BC��
��AB=2BC��
B���֣�10�֣����������MN=
|
|
|
��
|
|
|
����á�ABC����������1����A1B1C1�������|k|����������֪��|k|=2��1=2��
����k��ֵΪ2��-2��
C�⣺��2=2��cos�ȣ�Բ��=2cos�ȵ���ͨ����Ϊ��x2+y2=2x����x-1��2+y2=1��
ֱ��3��cos��+4��sin��+a=0����ͨ����Ϊ��3x+4y+a=0��
��Բ��ֱ�����У�����
| |3•1+4•0+a| | ||
|
��ã�a=2����a=-8��
D������һ��֤����a3+b3-
| ab |
| a |
| a |
| b |
| b |
| b |
| a |
=(
| a |
| b |
| a |
| b |
=(
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
��Ϊʵ��a��b��0��(
| a |
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
������ʽ��0������a3+b3��
| ab |
����������֤������a��b�ǷǸ�ʵ���������a3+b3-
| ab |
=a2
| a |
| a |
| b |
| b |
| b |
| a |
=(
| a |
| b |
| a |
| b |
��a��bʱ��
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
��a��bʱ��
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
����a3+b3��
| ab |
������������Ҫ���������Ρ�Բ���й�֪ʶ������������֤��������ͼ���ھ����Ӧ�ı任�µı仯�ص㣬������������������������ߵļ����귽�̵Ȼ���֪ʶ������ת��������������������Ҳ���������������ͨ���̵��������ϵ������Ҫ�ụ��ת��������ʵ�����ѡ��ͬ�ķ��̽�����⣬��Ҳ��ÿ��߿��ؿ����ȵ����⣮

��ϰ��ϵ�д�
�����Ŀ
 ѡ���Ȿ�����A��B��C��D��С�⣬��ѡ������ ���� ����ÿС��10�֣�����20�֣�
ѡ���Ȿ�����A��B��C��D��С�⣬��ѡ������ ���� ����ÿС��10�֣�����20�֣� ��2013•��Ǩһģ����ѡ���⡿�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
��2013•��Ǩһģ����ѡ���⡿�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮 ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮 ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮
ѡ���⣬�������A��B��C��D��С�⣬��ѡ���������⣬������Ӧ�Ĵ����������������������������ǰ�������֣����ʱӦд������˵����֤�����̻����㲽�裮