题目内容
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.(几何证明选讲)
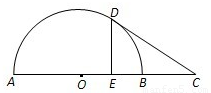
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
B.(矩阵与变换)
已知矩阵
|
|
C.(极坐标与参数方程)
在平面直角坐标系xOy中,已知点A(1,-2)在曲线
|
D.(不等式选讲)
设a1,a2,a3均为正数,且a1+a2+a3=1,求证:
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
分析:A、连接OD,则OD⊥DC,先确定∠ODE=30°,再在Rt△ODC中,可求BC的长;
B.根据二阶矩阵的特征值与特征向量的概念,建立方程组,即可求得结论;
C.化参数方程为普通方程,将点A(1,-2)代入,即可求得p的值;
D.a1,a2,a3均为正数,且a1+a2+a3=1>0,利用基本不等式即可证明.
B.根据二阶矩阵的特征值与特征向量的概念,建立方程组,即可求得结论;
C.化参数方程为普通方程,将点A(1,-2)代入,即可求得p的值;
D.a1,a2,a3均为正数,且a1+a2+a3=1>0,利用基本不等式即可证明.
解答:A、解:连接OD,则OD⊥DC,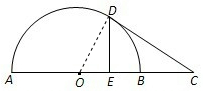
在Rt△OED中,OE=
OB=
OD,所以∠ODE=30°,
在Rt△ODC中,∠DCO=30°,由DC=2得OD=DCtan30°=
,
所以BC=
.
B.解:由二阶矩阵的特征值与特征向量的概念知
=b
,
所以
,解得a=1,b=3.
C.解:由
(t为参数,p为正常数),消去参数t得y2=2px,将点A(1,-2)代入y2=2px得p=2.
D.证明:因为a1,a2,a3均为正数,且a1+a2+a3=1>0,
所以
+
+
=(a1+a2+a3)(
+
+
)≥3(a1a2a3)
•3(
)
=9,
当且仅当a1=a2=a3=
时等号成立,
所以
+
+
≥9.

在Rt△OED中,OE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ODC中,∠DCO=30°,由DC=2得OD=DCtan30°=
2
| ||
| 3 |
所以BC=
2
| ||
| 3 |
B.解:由二阶矩阵的特征值与特征向量的概念知
|
|
|
所以
|
C.解:由
|
D.证明:因为a1,a2,a3均为正数,且a1+a2+a3=1>0,
所以
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| 3 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| 3 |
当且仅当a1=a2=a3=
| 1 |
| 3 |
所以
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
点评:本题是选考内容.A.主要考查三角形、圆的有关知识,考查推理论证、运算求解能力;B\主要考查二阶矩阵的特征值与特征向量,考查运算求解能力;C主要考查参数方程,考查运算求解能力;D主要考查证明不等式的基本方法,考查推理论证能力.

练习册系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 选修4-1:几何证明选讲
选修4-1:几何证明选讲 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。 。
。 ,求矩阵A.
,求矩阵A.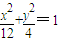 在第一象限处的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M、N,求矩形PMON周长最大值时点P的坐标.
在第一象限处的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M、N,求矩形PMON周长最大值时点P的坐标.
 的属于特征值b的一个特征向量为
的属于特征值b的一个特征向量为 ,求实数a、b的值.
,求实数a、b的值. (t为参数,p为正常数),求p的值.
(t为参数,p为正常数),求p的值.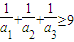 .
.