题目内容
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.A.(几何证明选讲)
如图,已知两圆交于A、B两点,过点A、B的直线分别与两圆交于P、Q和M、N.求证:PM∥QN.
B.(矩阵与变换)
已知矩阵A的逆矩阵A-1=
|
C.(极坐标与参数方程)
在平面直角坐标系xOy中,过椭圆
| x2 |
| 12 |
| y2 |
| 4 |
D.(不等式选讲)
已知关于x的不等式|x-a|+1-x>0的解集为R,求实数a的取值范围.
分析:A:先连接AB,利用圆的性质易得∠ABN和∠APM相等,及∠ABN和∠AQN互补,从而得到∠APM+∠AQN=π,再结合点P,A,Q三点共线,即得.
B:根据已知条件,求出矩阵M,由M•M-1=E,列出关于矩陈M中参数的方程组即可求得M.
C:先设
(α为参数),将矩形PMON周长表示成参数的三角函数的形式,利用三角函数的有啥界性即可求出矩形PMON周长取最大值;
D.对x分情况进行讨论:若x-1<0,则a∈R;若x-1≥0,即(a-1)[(a+1)-2x]>0对任意的x∈[1,+∞)恒成立,列出关于a的不等关系即可求出实数a的取值范围.
B:根据已知条件,求出矩阵M,由M•M-1=E,列出关于矩陈M中参数的方程组即可求得M.
C:先设
|
D.对x分情况进行讨论:若x-1<0,则a∈R;若x-1≥0,即(a-1)[(a+1)-2x]>0对任意的x∈[1,+∞)恒成立,列出关于a的不等关系即可求出实数a的取值范围.
解答: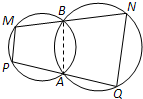 解:A.连接AB,易得∠ABN=∠APM,∠ABN+∠AQN=π,
解:A.连接AB,易得∠ABN=∠APM,∠ABN+∠AQN=π,
所以∠APM+∠AQN=π,
又点P,A,Q三点共线,
故PM∥QN.
B.设A=
,则由AA-1=E得
=
,
解得
所以A=
.
C.设
(α为参数),
则矩形PMON周长的一半为:2
cosα+2sinα=4sin(α+
),
所以,当α=
时,矩形PMON周长取最大值4×2=8,
此时,点P(3,1).
D.证明:若x-1<0,则a∈R;
若x-1≥0,则(x-a)2>(x-1)2对任意的x∈[1,+∞)恒成立,
即(a-1)[(a+1)-2x]>0对任意的x∈[1,+∞)恒成立,
所以
或
对任意的x∈[1,+∞)恒成立,
解得a<1.
 解:A.连接AB,易得∠ABN=∠APM,∠ABN+∠AQN=π,
解:A.连接AB,易得∠ABN=∠APM,∠ABN+∠AQN=π,所以∠APM+∠AQN=π,
又点P,A,Q三点共线,
故PM∥QN.
B.设A=
|
|
|
|
解得
|
|
C.设
|
则矩形PMON周长的一半为:2
| 3 |
| π |
| 3 |
所以,当α=
| π |
| 6 |
此时,点P(3,1).
D.证明:若x-1<0,则a∈R;
若x-1≥0,则(x-a)2>(x-1)2对任意的x∈[1,+∞)恒成立,
即(a-1)[(a+1)-2x]>0对任意的x∈[1,+∞)恒成立,
所以
|
|
解得a<1.
点评:本题主要考查圆的有关知识、逆矩阵、解绝对值不等式、椭圆的参数方程的基本方法,考查运算求解的能力.难度不大,做题要仔细.

练习册系列答案
相关题目
 选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤.
选作题,本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.解答时应写出文字说明、证明过程或演算步骤. 选修4-1:几何证明选讲
选修4-1:几何证明选讲 ,N=
,N= ,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。
,点A、B、C在矩阵MN对应的变换下得到点分别为A1、B1、C1,△A1B1C1的面积是△ABC面积的2倍,求k的值。 。
。 ,求矩阵A.
,求矩阵A.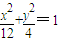 在第一象限处的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M、N,求矩形PMON周长最大值时点P的坐标.
在第一象限处的一点P(x,y)分别作x轴、y轴的两条垂线,垂足分别为M、N,求矩形PMON周长最大值时点P的坐标.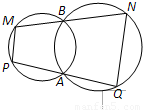
 的属于特征值b的一个特征向量为
的属于特征值b的一个特征向量为 ,求实数a、b的值.
,求实数a、b的值. (t为参数,p为正常数),求p的值.
(t为参数,p为正常数),求p的值.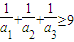 .
.