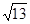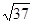题目内容
在△ABC中,a,b,c分别为角A,B,C的对边,已知a、b、c成等比数列,且a2-c2=ac-bc,则A=________,△ABC的形状为________.
60° 正三角形
∵a、b、c成等比数列,∴b2=ac.
又a2-c2=ac-bc,∴b2+c2-a2=bc.
在△ABC中,由余弦定理得cos A=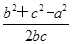 =
=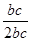 =
=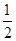 ,∴A=60°.
,∴A=60°.
由b2=ac,即a=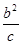 ,代入a2-c2=ac-bc,
,代入a2-c2=ac-bc,
整理得(b-c)(b3+c3+cb2)=0,
∴b=c,∴△ABC为正三角形.
又a2-c2=ac-bc,∴b2+c2-a2=bc.
在△ABC中,由余弦定理得cos A=
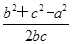 =
=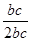 =
=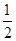 ,∴A=60°.
,∴A=60°.由b2=ac,即a=
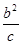 ,代入a2-c2=ac-bc,
,代入a2-c2=ac-bc,整理得(b-c)(b3+c3+cb2)=0,
∴b=c,∴△ABC为正三角形.

练习册系列答案
相关题目
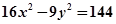 ,
,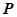 在双曲线上,满足
在双曲线上,满足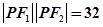 ,求
,求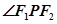 的大小.
的大小.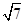 ,BC=2,B=60°,则边BC上的高为________.
,BC=2,B=60°,则边BC上的高为________.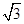 sin A)cos B=0.
sin A)cos B=0. 且满足
且满足 ,则
,则 _________.
_________.



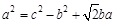 ,则∠C=( )
,则∠C=( )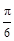
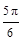

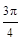
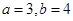 ,∠C=
,∠C=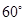 , 则边 c 的值等于( )
, 则边 c 的值等于( )