题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,已知cos C+(cos A-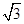 sin A)cos B=0.
sin A)cos B=0.
(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
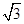 sin A)cos B=0.
sin A)cos B=0.(1)求角B的大小;
(2)若a+c=1,求b的取值范围.
(1)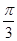 (2)
(2) ≤b<1.
≤b<1.
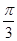 (2)
(2) ≤b<1.
≤b<1.(1)由已知得-cos(A+B)+cos Acos B-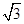 sin Acos B=0,即有sin Asin B-
sin Acos B=0,即有sin Asin B-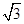 sin Acos B=0,因为sin A≠0,所以sin B-
sin Acos B=0,因为sin A≠0,所以sin B-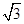 cos B=0,即
cos B=0,即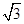 cos B=sin B.
cos B=sin B.
所以tan B=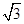 ,又因为0<B<π,所以B=
,又因为0<B<π,所以B=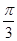 .
.
(2)由余弦定理得b2=a2+c2-2accos B,
因为a+c=1,cos B= ,
,
所以b2=(a+c)2-3ac≥(a+c)2-3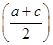 2=
2= (a+c)2=
(a+c)2= ,∴b≥
,∴b≥ .
.
又a+c>b,∴b<1,∴ ≤b<1.
≤b<1.
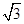 sin Acos B=0,即有sin Asin B-
sin Acos B=0,即有sin Asin B-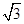 sin Acos B=0,因为sin A≠0,所以sin B-
sin Acos B=0,因为sin A≠0,所以sin B-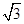 cos B=0,即
cos B=0,即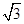 cos B=sin B.
cos B=sin B.所以tan B=
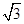 ,又因为0<B<π,所以B=
,又因为0<B<π,所以B=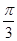 .
.(2)由余弦定理得b2=a2+c2-2accos B,
因为a+c=1,cos B=
 ,
,所以b2=(a+c)2-3ac≥(a+c)2-3
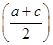 2=
2= (a+c)2=
(a+c)2= ,∴b≥
,∴b≥ .
.又a+c>b,∴b<1,∴
 ≤b<1.
≤b<1.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
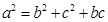 .
.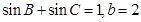 ,试求△ABC的面积.
,试求△ABC的面积. 中,若
中,若 ,则
,则 等于( )
等于( )

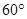
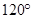
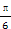 ,S△ABC=
,S△ABC= ,则b= .
,则b= .

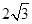
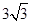
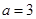 ,
,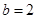 ,
,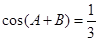 ,则
,则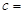 ( )
( )


