题目内容
已知双曲线的方程是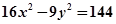 ,
,
(1)求此双曲线的焦点坐标、离心率和渐近线方程;
(2)点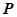 在双曲线上,满足
在双曲线上,满足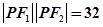 ,求
,求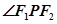 的大小.
的大小.
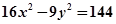 ,
,(1)求此双曲线的焦点坐标、离心率和渐近线方程;
(2)点
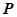 在双曲线上,满足
在双曲线上,满足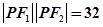 ,求
,求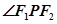 的大小.
的大小.(1) ,
, ,
, ;(2)
;(2)
 ,
, ,
, ;(2)
;(2)
试题分析:(1)将双曲线方程化为标准方程
 ,所以
,所以 ,焦点
,焦点 ,离心率为
,离心率为 ,渐近线方程为
,渐近线方程为 ;(2)在
;(2)在 中,
中, =10,又知道另外两边
=10,又知道另外两边 、
、 的关系:
的关系: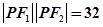 ,求
,求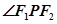 ,可想到余弦定理,利用余弦定理
,可想到余弦定理,利用余弦定理 ,又想到双曲线的定义
,又想到双曲线的定义 ,所以继续变形为
,所以继续变形为 =0,所以
=0,所以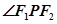 =
= .
.试题解析:(1)双曲线方程化为标准方程
 ,所以
,所以 ,∴焦点为
,∴焦点为 ,离心率为
,离心率为 ,渐近线方程为
,渐近线方程为 ;
;(2)因为点
 在双曲线上,所以
在双曲线上,所以 ,在
,在 中,
中, =
= =0,∴
=0,∴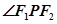 =
= .
.
练习册系列答案
相关题目
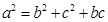 .
.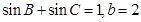 ,试求△ABC的面积.
,试求△ABC的面积.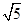 ,底面ABCD是边长为2的正方形,则CD与PA
,底面ABCD是边长为2的正方形,则CD与PA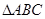 中,
中,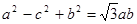 ,则∠C=______.
,则∠C=______. 中,若
中,若 ,
, ,
, ,则
,则 .
.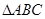 的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且
的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,则
,则 +
+ 的值是________.
的值是________.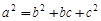 ,则角A等于( )
,则角A等于( )


