题目内容
已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈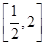 时,函数f(x)=x+
时,函数f(x)=x+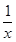 >
> 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
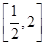 时,函数f(x)=x+
时,函数f(x)=x+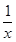 >
> 恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.
恒成立.如果p或q为真命题,p且q为假命题,求c的取值范围.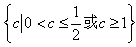
解:由命题p为真知,0<c<1,
由命题q为真知,2≤x+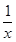 ≤
≤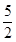 ,
,
要使此式恒成立,需 <2,即c>
<2,即c>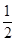 ,
,
若p或q为真命题,p且q为假命题,
则p、q中必有一真一假,
当p真q假时,
c的取值范围是0<c≤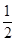 ;
;
当p假q真时,c的取值范围是c≥1.
综上可知,c的取值范围是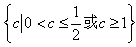 .
.
由命题q为真知,2≤x+
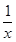 ≤
≤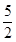 ,
,要使此式恒成立,需
 <2,即c>
<2,即c>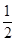 ,
,若p或q为真命题,p且q为假命题,
则p、q中必有一真一假,
当p真q假时,
c的取值范围是0<c≤
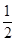 ;
;当p假q真时,c的取值范围是c≥1.
综上可知,c的取值范围是
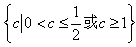 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
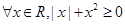 ”的否定是( )
”的否定是( )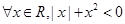
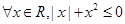
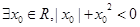
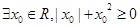
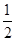 ,
,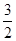 ]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.
]内恒成立.若命题“p且q”是假命题,求实数a的取值范围.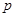 :$
:$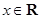 ,
,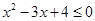 ,则下列说法正确的是( )
,则下列说法正确的是( )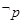 :$
:$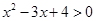 ,且
,且 p1)∧(
p1)∧( ;
; ;
; ,
, ,则“
,则“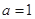 ”是“
”是“ ”的必要不充分条件;
”的必要不充分条件; ,
, 为单位向量,其夹角为
为单位向量,其夹角为 ,若
,若 ,则
,则 .
.