题目内容
9.等差数列{an}的前n项和Sn,已知a11-a8=3,S11-S8=3,当Sn=0时,n=17.分析 设等差数列{an}的公差是d,由a11-a8=3求得等差数列的公差,代入S11-S8=3求得首项,利用等差数列的前n项和公式化简Sn=0,再求出n的值.
解答 解:设等差数列{an}的公差是d,
由a11-a8=3d=3得,d=1,
∵S11-S8=a11+a10+a9=3a1+27d=3,∴a1=-8,
由Sn=0得,nan+$\frac{n(n-1)}{2}×d$=0,则-8n+$\frac{n(n-1)}{2}$=0,
解得n=17,
故答案为:17.
点评 本题考查等差数列的通项公式和前n项和公式的合理运用,是基础题.

练习册系列答案
相关题目
20.函数f(x)=$\frac{lnx}{x}$(x>0)( )
| A. | 在(0,+∞)上是减函数 | |
| B. | 在(0,+∞)上是减函数 | |
| C. | 在(0,e)上是增函数,在(e,+∞)上是减函数 | |
| D. | 在(0,e)上是减函数,在(e,+∞)上是增函数 |
4.在△ABC中,a=4sin10°,b=sin50°,∠C=70°,则S△ABC=( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
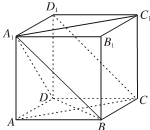 已知正方体ABCD-A1B1C1D1.
已知正方体ABCD-A1B1C1D1.