题目内容
某经销商试销A、B两种商品一个月(30天)的记录如下:
| 日销售量(件) | 0 | 1 | 2 | 3 | 4 | 5 |
| 商品A的频数 | 2 | 5 | 7 | 7 | 5 | 4 |
| 商品B的频数 | 4 | 4 | 6 | 8 | 5 | 3 |
(Ⅰ)求B商品日销售量不超过3件的概率;
(Ⅱ)由于某种原因,该商家决定只选择经销A、B商品的一种,你认为应选择哪种商品,说明理由。
(Ⅰ) (Ⅱ)应选择经销商品A
(Ⅱ)应选择经销商品A
解析试题分析:(Ⅰ)根据题意B商品日销售量不超过3件拆分为B商品日销售量为0,1,2,3这四个互斥事件,逐一求出其概率相加就可;(Ⅱ)比较商品A,B的日均利润平均值的大小,选平均值较大者.
试题解析:(Ⅰ)记事件“商品B日销售量为i件”为Bi,i=0,1,2,3,4,5.
商品B日销售量不超过3件的概率为
P=P(B0)+P(B1)+P(B2)+P(B3)= +
+ +
+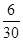 +
+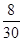 =
= .
.
(Ⅱ)商品A,B的日均利润平均值分别为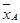 =40×
=40× =
= ,
, =40×
=40×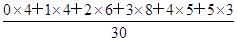 =100,
=100,
因为 >
> ,所以应经销商品A.
,所以应经销商品A.
考点:1、古典概型;2、计算平均值.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
小王经营一家面包店,每天从生产商处订购一种品牌现烤面包出售.已知每卖出一个现烤面包可获利10元,若当天卖不完,则未卖出的现烤面包因过期每个亏损5元.经统计,得到在某月(30天)中,小王每天售出的现烤面包个数 及天数如下表:
及天数如下表:
售出个数 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
(Ⅰ)计算小王某天售出该现烤面包超过13个的概率;
(Ⅱ)若在今后的连续5天中,售出该现烤面包超过13个的天数大于3天,则小王决定增加订购量. 试求小王增加订购量的概率.
(Ⅲ)若小王每天订购14个该现烤面包,求其一天出售该现烤面包所获利润的分布列和数学期望.
某校50名学生参加智力答题活动,每人回答3个问题,答对题目个数及对应人数统计结果见下表:
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
(Ⅰ)从50名学生中任选两人,求两人答对题目个数之和为4或5的概率;
(Ⅱ)从50名学生中任选两人,用X表示这两名学生答对题目个数之差的绝对值,求随机变量X的分布列及数学期望EX.
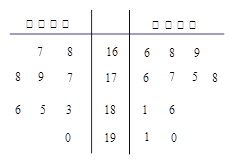
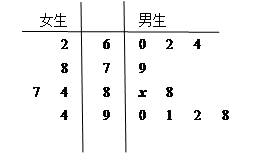
 ,求
,求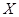 为选取女生的人数,求
为选取女生的人数,求
 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.