题目内容
 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则| 1 | ||
|
| 1 |
| |CA|2 |
| 1 |
| |CB|2 |
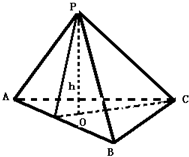
类比此性质,如图,在四面体P-ABC中,若PA,PB,PC两两垂直,
底面ABC上的高为h,则得到的一个正确结论是
| 1 |
| h2 |
| 1 |
| |PA|2 |
| 1 |
| |PB|2 |
| 1 |
| |PC|2 |
| 1 |
| h2 |
| 1 |
| |PA|2 |
| 1 |
| |PB|2 |
| 1 |
| |PC|2 |
分析:由平面图形中的二维性质类比推理出空间里三维的性质,故由平面性质:“若Rt△ABC的斜边AB上的高为h,则
=
+
”可以推断出一个在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,也存在一个相似的三维性质.
| 1 | ||
|
| 1 |
| |CA|2 |
| 1 |
| |CB|2 |
解答:解:∵在平面上的性质,若Rt△ABC的斜边AB上的高为h,则有
=
+
.”
我们类比到空间中,可以类比推断出:
在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,
有:
=
+
+
故答案为:
=
+
+
| 1 | ||
|
| 1 |
| |CA|2 |
| 1 |
| |CB|2 |
我们类比到空间中,可以类比推断出:
在四面体P-ABC中,若PA、PB、PC两两垂直,底面ABC上的高为h,
有:
| 1 |
| h2 |
| 1 |
| |PA|2 |
| 1 |
| |PB|2 |
| 1 |
| |PC|2 |
故答案为:
| 1 |
| h2 |
| 1 |
| |PA|2 |
| 1 |
| |PB|2 |
| 1 |
| |PC|2 |
点评:类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
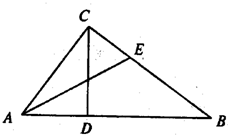 如图,在Rt△ABC中,∠C是直角,AC=3,BC=4,CD⊥AB于点D,∠A的平分线交CD于点M,交BC于点E,求:
如图,在Rt△ABC中,∠C是直角,AC=3,BC=4,CD⊥AB于点D,∠A的平分线交CD于点M,交BC于点E,求: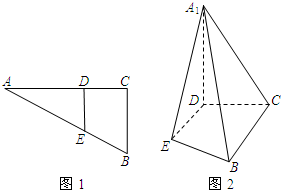 如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.
如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6.D、E分别是AC、AB上的点,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2.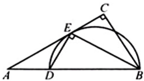 选修4-1:几何证明选讲
选修4-1:几何证明选讲