题目内容
在Rt△ABC中,∠C=90°,AC=BC=2,D是△ABC内切圆圆心,设P是⊙D外的三角形ABC区域内的动点,若
=λ
+μ
,则点(λ,μ)所在区域的面积为
-(
-
)π
-(
-
)π.
| CP |
| CA |
| CB |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
分析:建立直角坐标系,求出内切圆的半径,然后可求出点P所在区域的面积,从而可求出点(λ,μ)所在区域的面积.
解答:解: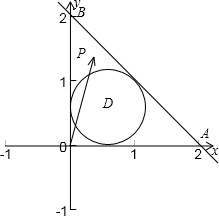 根据题意画出图象,以点C为坐标原点,CA为x轴,CB为y轴建立直接坐标系
根据题意画出图象,以点C为坐标原点,CA为x轴,CB为y轴建立直接坐标系
∵AB=2
,AC=BC=2,∠C=90°
∴△ABC内切圆的半径为
=2-
则⊙D外的三角形ABC区域面积为2-(6-4
)π
=λ
+μ
=(2λ,2μ)
则点(2λ,2μ)所在区域的面积为2-(6-4
)π
则点(λ,μ)所在区域的面积为点(2λ,2μ)所在区域的面积的
∴点(λ,μ)所在区域的面积为
-(
-
)π
故答案为:
-(
-
)π
 根据题意画出图象,以点C为坐标原点,CA为x轴,CB为y轴建立直接坐标系
根据题意画出图象,以点C为坐标原点,CA为x轴,CB为y轴建立直接坐标系∵AB=2
| 2 |
∴△ABC内切圆的半径为
| CA+CB-AB |
| 2 |
| 2 |
则⊙D外的三角形ABC区域面积为2-(6-4
| 2 |
| CP |
| CA |
| CB |
则点(2λ,2μ)所在区域的面积为2-(6-4
| 2 |
则点(λ,μ)所在区域的面积为点(2λ,2μ)所在区域的面积的
| 1 |
| 4 |
∴点(λ,μ)所在区域的面积为
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
故答案为:
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
点评:本题主要考查了平面向量的基本定理及其意义,以及直角三角形的内切圆等基础知识,同时考查了分析问题的能力和转化的思想,属于中档题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC=
如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,且AD:BD=9:4,则AC:BC= (几何证明选讲选做题)
(几何证明选讲选做题)